درس 4: قضیۀ هرون (محاسبۀ ارتفاعها و مساحت مثلث)
هندسه (2)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
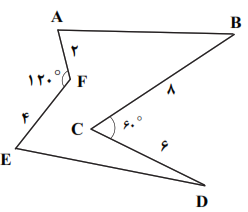
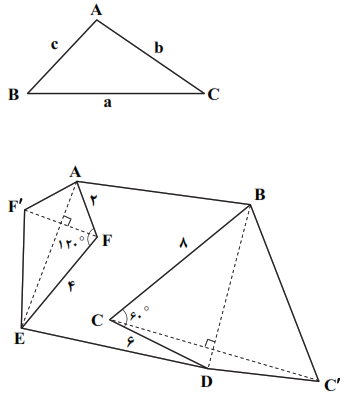
در شکل زیر اگر بخواهیم بدون تغییر محیط و تعداد اضلاع و با استفاده از تبدیل هندسی مناسب، مساحت شش ضلعی را افزایش دهیم، میزان افزایش مساحت چند برابر $\sqrt{3}$ است؟