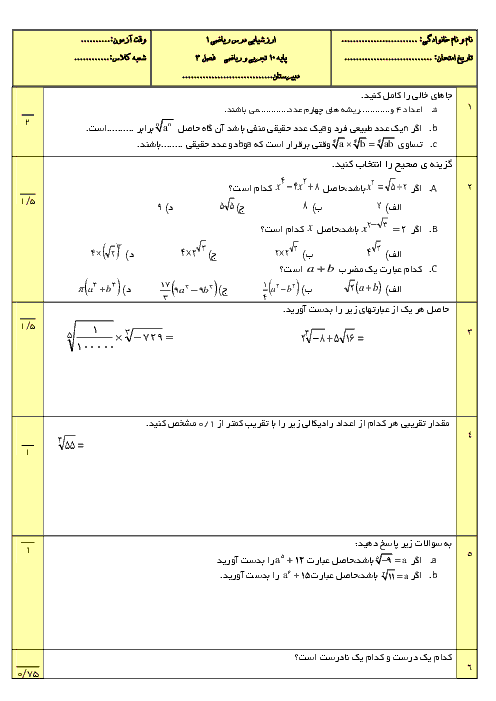
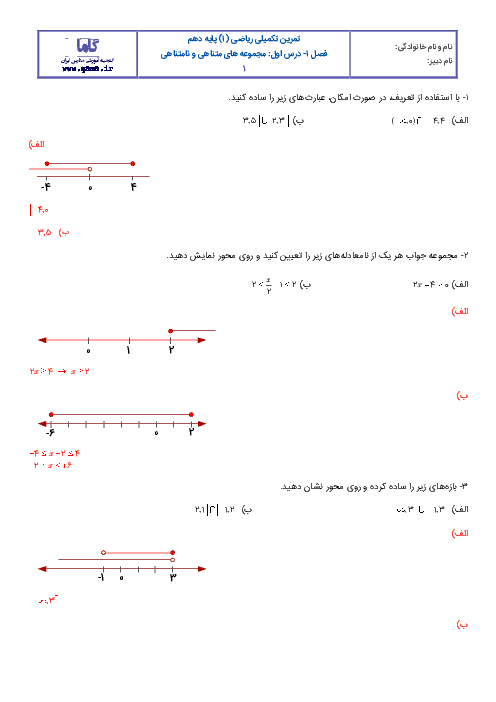
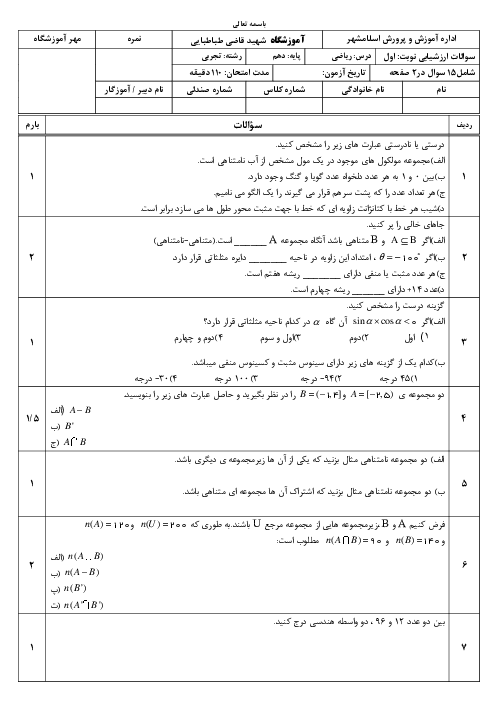
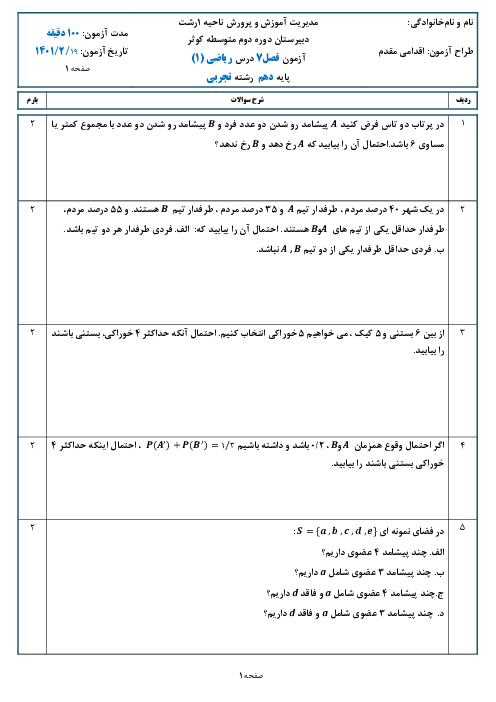
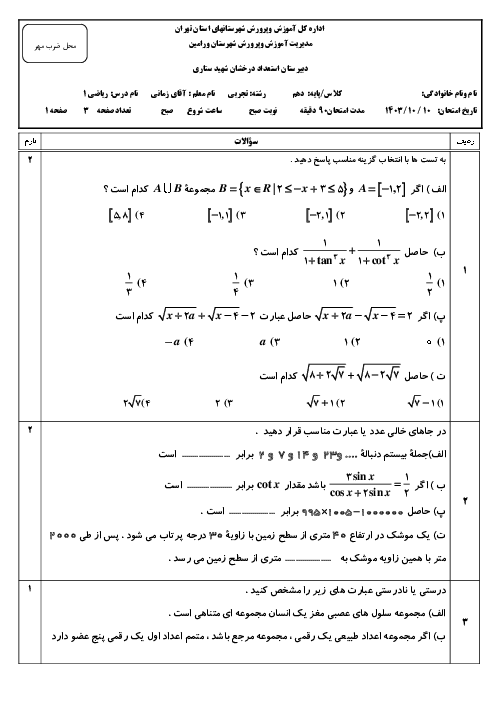
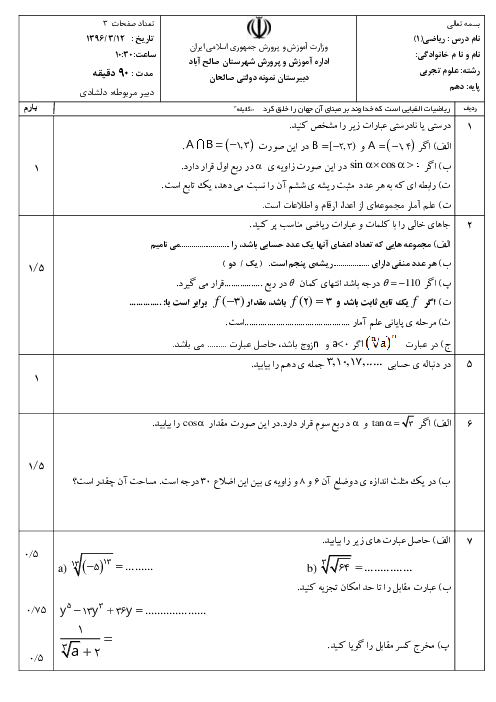درس 1: معادلۀ درجه دوم و روشهای مختلف حل آن
ریاضی (1)
دهم
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
اگر $\alpha$ و $\beta$ ریشههای معادلهی $b^{2}+ \sqrt {2}b- 4=0$ باشند، حاصل $\frac {\alpha}{\beta}$ کدام است؟ ($\alpha \gt \beta$)