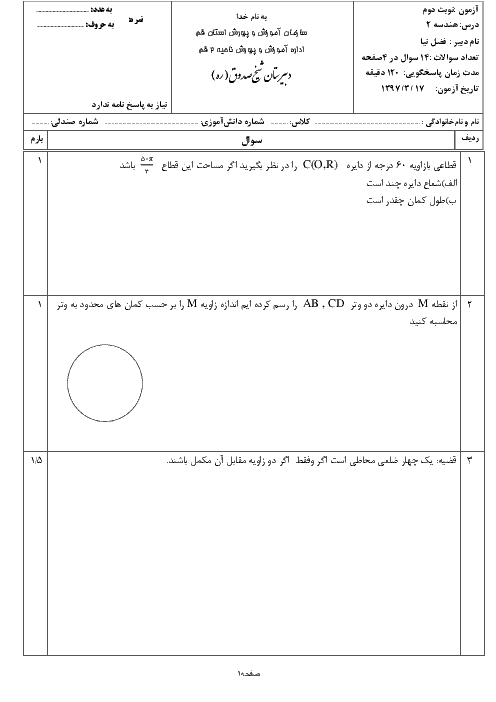
فرض کنید پارهخط $A'B'$ مجانس پارهخط AB در تجانس به مرکز O و نسبت تجانس k باشد. با توجه به شکل مقابل ثابت کنید:
الف) $\frac{{A'B'}}{{AB}} = k$
ب) اگر n ضلعی ${A'_1},{A'_2},...,{A'_n}$ مجانس n ضلعی ${A_1},{A_2},...,{A_n}$ باشد، ثابت کنید این دو n ضلعی باهم متشابهاند.
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!