وزنه‌ای به جرم را به فنر سبکی به طول که از سقف آسانسور ساکنی آویزان است، وصل می‌کنیم. بعد از رسیدن وزنه به حالت تعادل، فاصلهٔ آن از کف آسانسور است. اگر آسانسور…

گاما رو نصب کن!

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

پربازدیدها: #{{ tag.title }}

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

فیزیک و اندازه‌گیری فیزیک کنکور سراسری دوره دوم متوسطه- نظری علوم تجربی

وزنه‌ای به جرم $2kg$ را به فنر سبکی به طول $40cm$ که از سقف آسانسور ساکنی آویزان است، وصل می‌کنیم. بعد از رسیدن وزنه به حالت تعادل، فاصلهٔ آن از کف آسانسور $140cm$ است. اگر آسانسور با شتاب ثابت $2\frac{m}{{{s^2}}}$ رو به بالا شروع به حرکت کند، فاصلهٔ وزنه از کف آسانسور به $136cm$ می‌رسد. ثابت فنر چند نیوتون بر سانتی‌متر است؟ $(g = 10\frac{m}{{{s^2}}})$

1 )

$\frac{2}{3}$

2 )

$1$

3 )

$\frac{3}{2}$

4 )

$2$

نمایش پاسخ

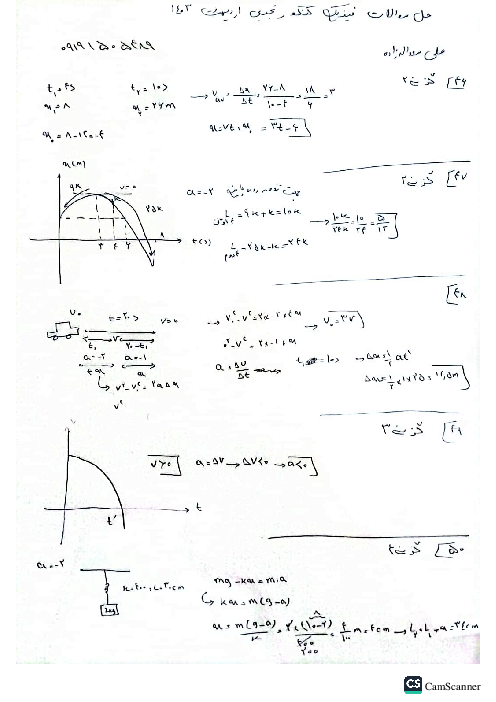
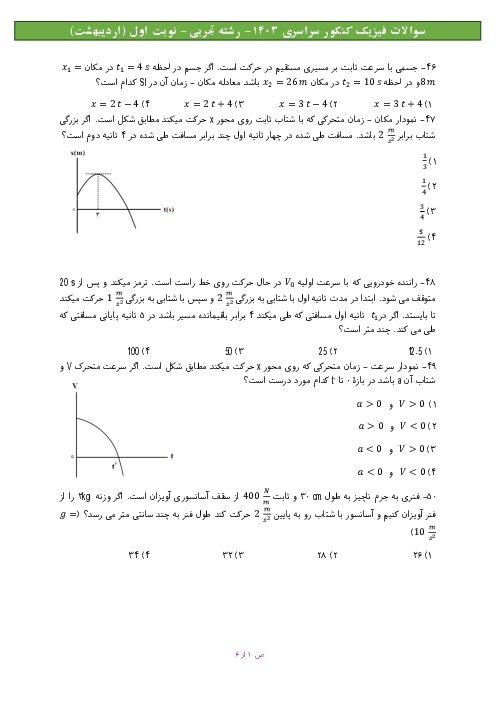
گام اول: پس از وصل‌کردن وزنه به فنر و رسیدن آن به حالت تعادل، فنر به اندازهٔ $\Delta {x_1}$ کشیده می‌شود؛ بنابراین داریم:

$k\Delta {x_1} = mg$

گام دوم: هنگامی که آسانسور با شتاب ثابت رو به بالا شروع به حرکت می‌کند، فاصلهٔ وزنه از کف آسانسور $140 - 136 = 4cm$ کاهش می‌یابد؛ بنابراین فنر در این حالت به اندازهٔ $\Delta {x_2} = 4cm$ دیگر کشیده شده است.

قانون دوم نیوتون را برای وزنه می‌نویسیم:

${F_{net}} = ma \Rightarrow F' - mg = ma$

$ \Rightarrow k(\Delta {x_2} + \Delta {x_1}) = mg + ma$

$k\Delta {x_1} = mg \to k\Delta {x_2} = ma \Rightarrow k \times 4 = 2 \times 2$

$ \Rightarrow k = 1N/cm$

تکنیک: از همان ابتدا می‌توانستیم بگوییم که پس از شروع به حرکت آسانسور، نیروی خالص وارد بر وزنه $k\Delta {x_2}$ است؛ بنابراین طبق قانون دوم نیوتون داریم:

${F_2} = ma \Rightarrow k\Delta {x_2} = ma$

$ \Rightarrow k \times 4 = 2 \times 2 \Rightarrow k = 1N/cm$