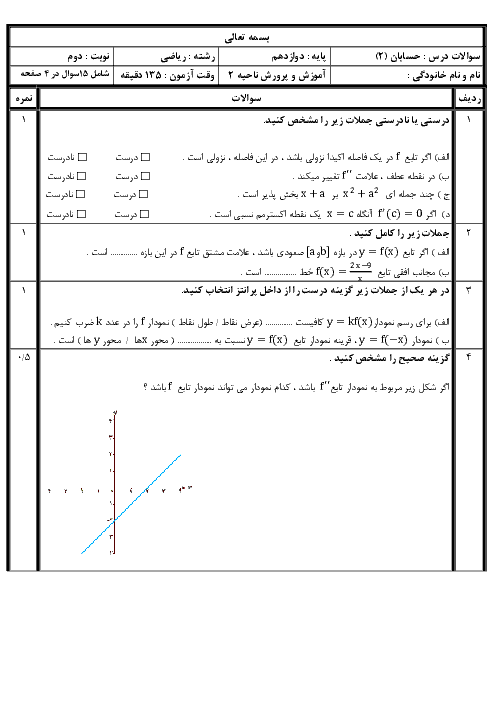
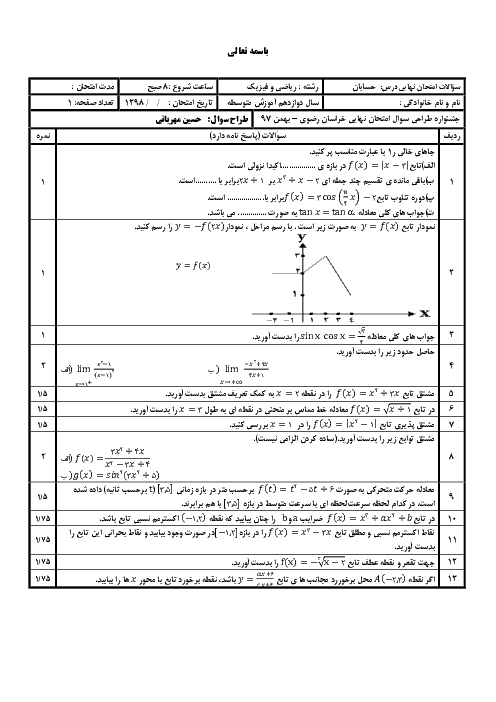
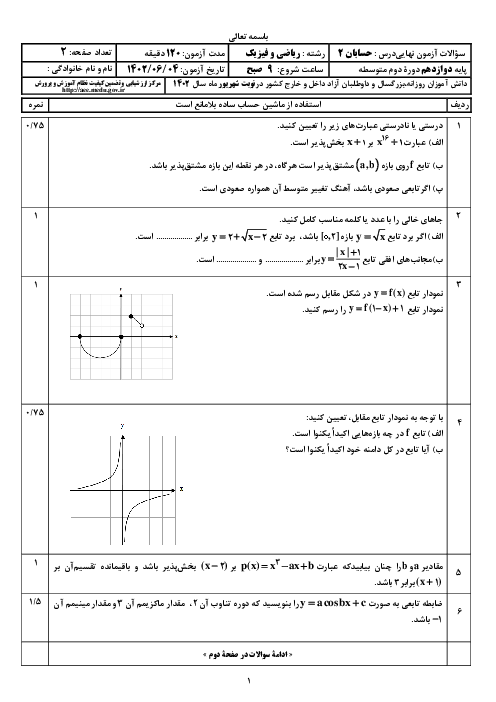
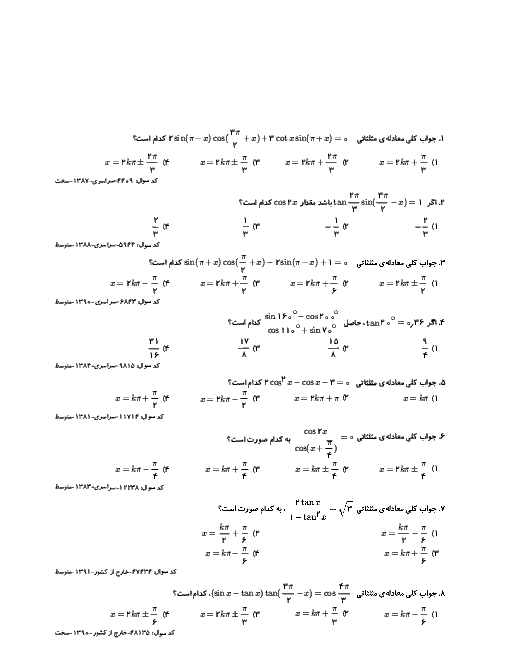اگر و نمودار تابع به شکل زیر باشد، آنگاه زوج مرتب کدام می‌تواند باشد؟ | حسابان (2) دوازدهم شماره 70780 - گاما

گاما رو نصب کن!

درحال دریافت اطلاعات ...

{{ successMsg }}

{{ errorMsg }}

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت اول گام به گام کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نمونه سوال تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم گزارش کارورزی

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

درس 1: تبدیل نمودار توابع حسابان (2) دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

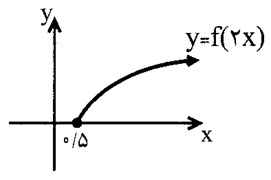
اگر $f(x)=\sqrt{ax+b}$ و نمودار تابع $y=f(2x)$ به شکل زیر باشد، آنگاه زوج مرتب $(a,b)$ کدام می‌تواند باشد؟

1 )

$(2,-4)$

2 )

$(1,-1)$

3 )

$(-1,1)$

4 )

$(4,-2)$

نمایش پاسخ

از آنجا که $f(\frac{2x}{2})=f(x)$، با دو برابر کردن طول نقاط تابع $y=f(2x)$، نمودار تابع $f(x)$ حاصل می‌شود. بنابراین:

بنابراین دامنهٔ تابع $f(x)$ بازهٔ $\left[ 1,+\infty \right]$ است. از طرفی دامنهٔ تابع $f(x)=\sqrt{ax+b}$ برابر است با:

$ax+b\ge 0\Rightarrow ax\ge -b$

$\xrightarrow{''a''\,mosbat}x\ge \frac{-b}{a}\Rightarrow {{D}_{f}}=\left[ \frac{-b}{a},+\infty ) \right.$

بنابراین $\frac{-b}{a}=1$ و نتیجه $a=-b$. توجه کنید چون $a$ مثبت است پس گزینهٔ $(2)$ صحیح است.

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

1401/07/13

عباس ابراهیمی علویجه

ویدیو دوره آموزشی، حسابان (2) دوازدهم دوره دوم متوسطه- نظری

مدرس: سید حجت طبائی

مدت دوره: 3 ساعت (5 فایل)

با گنجینه سوال، آزمون دلخواهتو بساز

سوپراستار

بسته ویژه نمره بیست: 15 دوره امتحان نهایی درس حسابان (2) دوازدهم

72 صفحه

بسته ویژه نمره بیست: 15 دوره امتحان نهایی درس حسابان (2) دوازدهم

ويژه نامه نوبت اول و…

سوپراستار

4 سری نمونه سؤال آمادگی امتحان نهایی (نوبت دوم) حسابان (2) دوازدهم ریاضی

8 صفحه

4 سری نمونه سؤال آمادگی امتحان نهایی (نوبت دوم) حسابان (2) دوازدهم ریاضی

کلاس دوازدهمی‌ها

آزمون حسابان 2 نوبت دی ماه 1403 دبیرستان تیزهوشان شهید هاشمی نژاد

6 صفحه

آزمون حسابان 2 نوبت دی ماه 1403 دبیرستان تیزهوشان شهید هاشمی نژاد

مجتبی محمدیان

امتحان نوبت اول حسابان (2) دوازدهم دبیرستان امام خمینی اردستان | دی 1401

4 صفحه

امتحان نوبت اول حسابان (2) دوازدهم دبیرستان امام خمینی اردستان | دی 1401

محمدحسین شادی زواره

جزوه دست نویس حسابان 2 - فصل 1

24 صفحه

جزوه دست نویس حسابان 2 - فصل 1

محمد شاهسون

آزمونک حسابان (2) دوازدهم دبیرستان دكتر طاهره صفار زاده | فصل 1: تابع

1 صفحه

آزمونک حسابان (2) دوازدهم دبیرستان دكتر طاهره صفار زاده | فصل 1: تابع

زهرا بازیار

نمونه سوال آزمون نوبت اول حسابان 2 دی ماه 1403 دبیرستان شهید رجایی

4 صفحه

نمونه سوال آزمون نوبت اول حسابان 2 دی ماه 1403 دبیرستان شهید رجایی

اردوان مختاری

جزوه و نکات کلیدی حسابان 2 با مثال های تشریحی و تست های کنکوری | فصل 4: مشتق

36 صفحه

جزوه و نکات کلیدی حسابان 2 با مثال های تشریحی و تست های کنکوری | فصل 4:…

بیتا سلیمانی امیری

مجموعه تست های تالیفی، کنکوری و آزمون های آزمایشی حسابان (2) دوازدهم | فصل 1: تابع

26 صفحه

مجموعه تست های تالیفی، کنکوری و آزمون های آزمایشی حسابان (2) دوازدهم |…

علی فقیهی

آزمون آمادگی امتحان نهایی حسابان (2) دوازدهم ریاضی + پاسخ | نمونه 1

2 صفحه

آزمون آمادگی امتحان نهایی حسابان (2) دوازدهم ریاضی + پاسخ | نمونه 1

کلاس دوازدهمی‌ها

موارد بیشتر

موارد بیشتر

ارسال فایل

آیا تابع می‌تواند هم نزولی هم صعودی باشد؟

منظور از صفر بیشتر و صفر کمتر چیست؟

تابع f(x)= 2√x-2 - k √x-1 یکنوا است. حدود k کدام است؟

موارد بیشتر

ارسال پرسش

موارد بیشتر