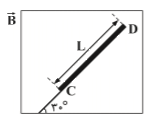
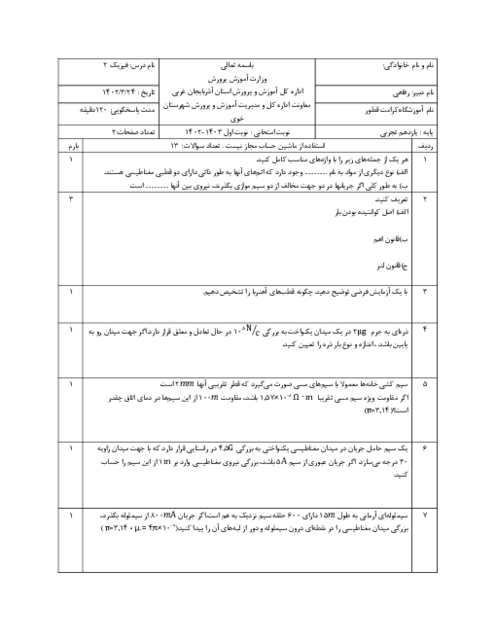
با استفاده از قانون دوم نيوتون، رابطهٔ اندازهٔ نيروی مغناطيسی وارد بر رسانای حامل جريان و رابطهٔ چگالی يک جسم همگن و توجه به اين مطلب كه تنها نيروی افقی وارد بر ميلهٔ فلزی، نيروی مغناطيسی ناشی از ميدان مغناطيسی يكنواخت است، داريم:

$F=ma\xrightarrow[m=\rho V=\rho AL=\rho \pi {{r}^{2}}L]{F=ILB\,\sin \alpha }ILB\,\sin \alpha =\rho \pi {{r}^{2}}La$

$a=\frac{IB\sin \alpha }{\rho \pi {{r}^{2}}}\,\,\,\,(1)$

با توجه به اينكه  $\alpha $ زاويهٔ حادهٔ جهت جريان با جهت بردار ميدان مغناطيسی است، در اين سؤال $\alpha ={{90}^{\circ }}$ است. با جايگذاری اعداد در رابطهٔ (1) داریم:

$a=\frac{IB\,\sin \alpha }{\rho \pi {{r}^{2}}}\xrightarrow[\rho =8\frac{g}{c{{m}^{3}}}=8000\frac{kg}{{{m}^{3}}}\,,\,r=\frac{D}{2}=5mm=5\times {{10}^{-3}}m]{I=40A\,,\,B=1/2\times {{10}^{-2}}T\,,\,\alpha ={{90}^{\circ }}\,,\,\pi \simeq 3}$

$a=\frac{40\times 1/2\times {{10}^{-2}}\times \sin {{90}^{\circ }}}{8000\times 3\times (5\times {{10}^{-3}})}\Rightarrow a=0/8\frac{m}{{{s}^{2}}}$

توجه داشته باشيد كه به دليل حذف شدن $L$ از طرفين رابطه، برای محاسبهٔ $a$ به طول ميلهٔ فلزی $(L)$ نیاز نداریم.