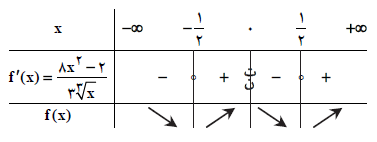
نکته: فرض کنیم $c$ طول نقطه‌ی بحرانی تابع $f$ باشد، که $f$ در $c$ پیوسته است و همچنین $f$ در یک همسایگی محذوف $c$ مشتق‌پذیر باشد.

الف) اگر علامت ${f}'$ در $x=c$ از مثبت به منفی تغییر کند، آن‌گاه $x=c$ طول نقطه‌ی ماکزیمم نسبی تابع $f$ است.

ب) اگر علامت ${f}'$ در $x=c$ از منفی به مثبت تغییر کند، آن‌گاه $x=c$ طول نقطه‌ی مینیمم نسبی تابع $f$ است.

تابع $f(x)=({{x}^{2}}-1)\sqrt[3]{{{x}^{2}}}$ در کل $R$ پیوسته است و داریم:

${f}'(x)=2x\sqrt[3]{{{x}^{2}}}+\frac{2}{3\sqrt[3]{x}}({{x}^{2}}-1)=\frac{6{{x}^{2}}+2{{x}^{2}}-2}{3\sqrt[3]{x}}=\frac{8{{x}^{2}}-2}{3\sqrt[3]{x}}$ 

حال مشتق را تعیین علامت می‌کنیم:

$8{{x}^{2}}-2=0\Rightarrow {{x}^{2}}=\frac{1}{4}\Rightarrow x=\pm \frac{1}{2}$ 

$3\sqrt[3]{x}=0\Rightarrow x=0$ 

نقاط $x=0$ و $x=\pm \frac{1}{2}$ نقاط بحرانی تابع هستند و داریم:

تابع در نقاط $x=\pm \frac{1}{2}$ مینیمم نسبی و در نقطه‌ی  $x=0$ ماکزیمم نسبی دارد.