الف)

${{F}_{E}}=\left| q \right|E=\left( 50\times {{10}^{-9}} \right)\times \left( 8\times {{10}^{5}} \right)=400\times {{10}^{-4}}=4\times {{10}^{-2}}N$

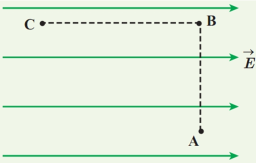
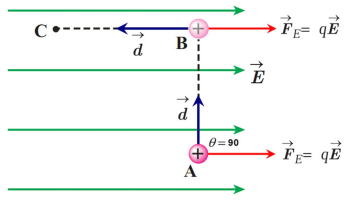
ب) کار این نیرو را می‌توان در دو مسیر AB و BC به دست آورد سپس آنها را با هم جمع کرد.

$A\to B:{{W}_{{{F}_{E}}}}={{F}_{_{E}}}d\cos \theta \to {{W}_{{{F}_{E}}}}={{F}_{E}}d\cos 90\to {{W}_{{{F}_{E}}}}=0$
$B\to C:{{W}_{{{F}_{E}}}}={{F}_{E}}d\cos \theta \to {{W}_{{{F}_{E}}}}=\left( 4\times {{10}^{-2}} \right)\times 0/4\cos 180\to {{W}_{{{F}_{E}}}}=-1/6\times {{10}^{-2j}}$
$A\to B\to C:W={{W}_{AB}}+{{W}_{BC}}=0+-1/6\times {{10}^{-2}}=-1/6\times {{10}^{-2}}j$

پ) این قسمت را می‌توان با دو روش به دست آورد:
روش اول، اندازه‌ی تغییر انرژی پتانسیل الکتریکی برابر است با منفی کار میدان الکتریکی، کار میدان الکتریکی را در قسمت الف به دست آوردیم بنابراین داریم:

$\Delta {{U}_{E}}=-{{W}_{{{F}_{E}}}}=-(1/6\times {{10}^{-2}})=1/6\times {{10}^{-2}}j$

روش دوم: استفاده از رابطه‌ی $\Delta {{U}_{E}}=-\left| q \right|Ed\cos \theta $ در این رابطه $\theta $ زاویه بین نیرو و جابه جایی است و در مسیر عمود بر میدان، مقدار آن برابر با صفر است.

$\Delta {{U}_{E}}=-\left| q \right|Ed\cos \theta =-\left( 50\times {{10}^{-9}} \right)\times \left( 8\times {{10}^{5}} \right)\times 0/4\times \cos 180=1/6\times {{10}^{-2j}}$