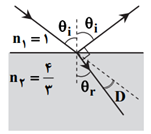
پرتوی نوری از هوا بهطور مايل به سطح آب با ضريب شكست $n=\frac{4}{3}$ میتابد. بخشی از آن بازتاب و بخش ديگر پس از شكست وارد آب میشود. اگر پرتو بازتاب عمود بر پرتو شكست باشد، پرتو پس از ورود به آب چند درجه و چگونه منحرف میشود؟ $(\operatorname{Cos}{{37}^{{}^\circ }}=0/8,\operatorname{Sin}{{37}^{{}^\circ }}=0/6)$
1 )
37 درجه به خط عمود نزديک میشود.
16 درجه به خط عمود نزديک میشود.
3 )
37 درجه از خط عمود دور میشود.
4 )
16 درجه از خط عمود دور میشود.
پاسخ تشریحی :