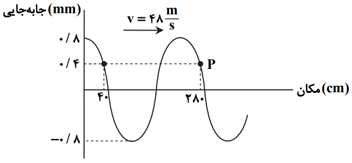
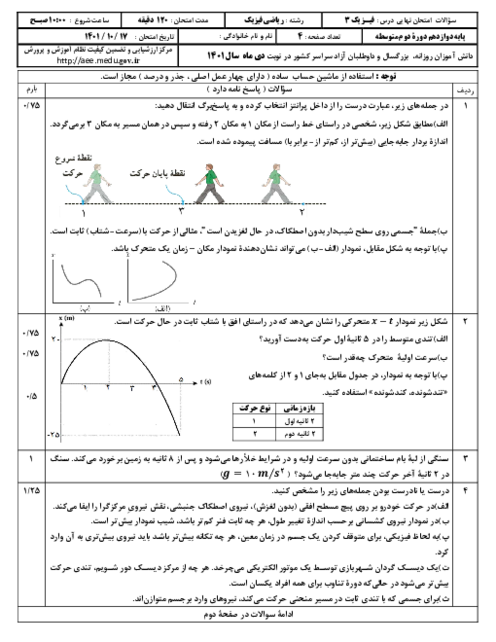$\lambda =280-40=240cm=2/4m$
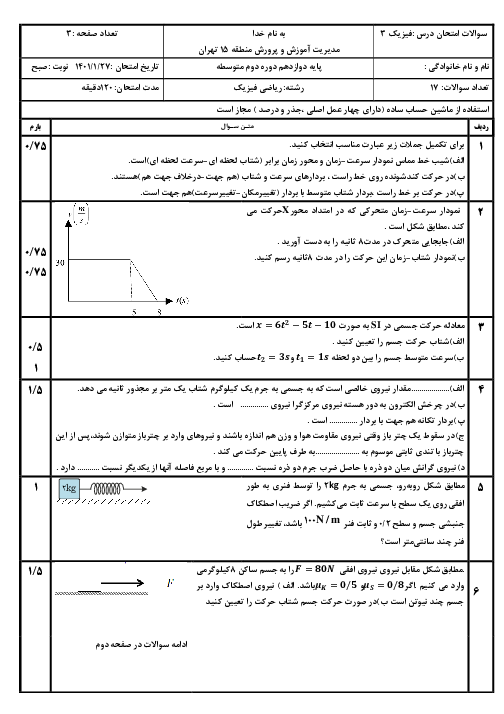
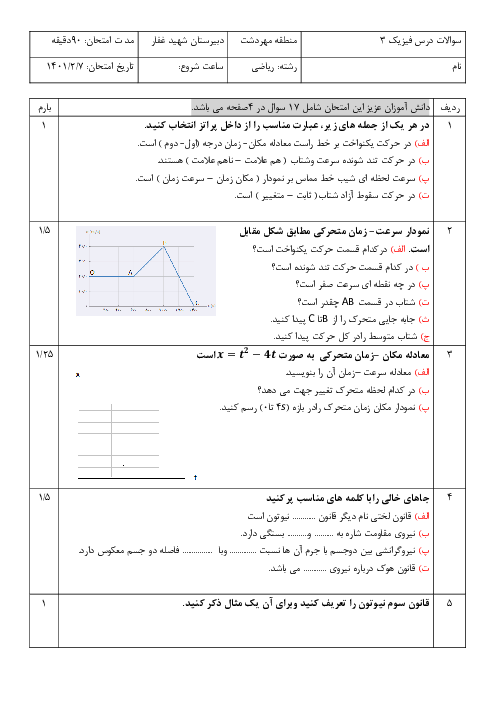
$\lambda =v.T\Rightarrow 2/4=48T\Rightarrow T=\frac{2/4}{48}=\frac{1}{20}s$
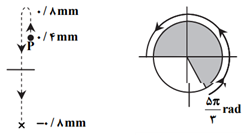
نقطهٔ $P$ یک نوسانگر است که باید از وضعیت $\frac{+1}{2}A$ تا $A$ و از آنجا تا $-A$ حرکت کند تا مسافتی برابر 20 میلیمتر طی شود. (چرا؟)
$y=A\operatorname{Cos}\omega t\Rightarrow \left\{ \begin{matrix} y=\frac{A}{2}\Rightarrow \operatorname{Cos}\omega t=\frac{1}{2}\Rightarrow \omega t=5\frac{\pi }{3}rad \\ y=A\Rightarrow \omega t=2\pi rad \\ y=-A\Rightarrow \omega t=3\pi rad \\ \end{matrix} \right.$
پس باید $\omega t$ از $\frac{5\pi }{3}$ رادیان تا $3\pi $ رادیان تغییر کند.
$\left. \begin{matrix} \omega {{t}_{1}}=\frac{5\pi }{3} \\ \omega {{t}_{2}}=3\pi \\ \end{matrix} \right\}\Rightarrow \omega ({{t}_{2}}-{{t}_{1}})=3\pi -\frac{5\pi }{3}=\frac{4\pi }{3}$
${{t}_{2}}-{{t}_{1}}=\frac{\frac{4\pi }{3}}{\frac{2\pi }{T}}=\frac{2}{3}\times \frac{1}{20}=\frac{1}{30}s=\frac{100}{3}ms$