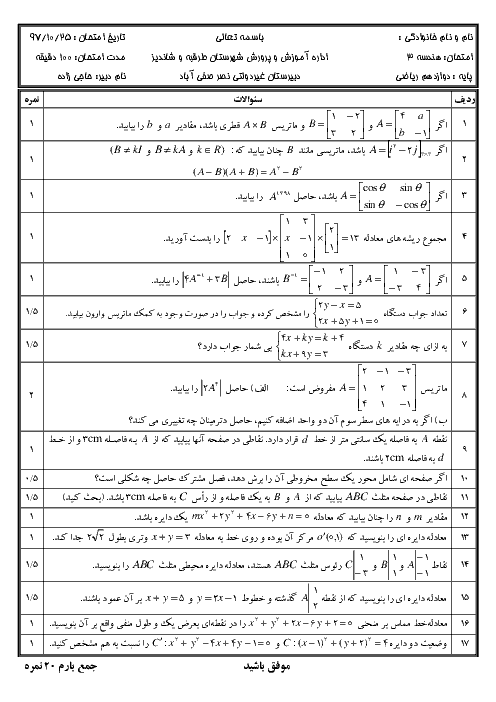
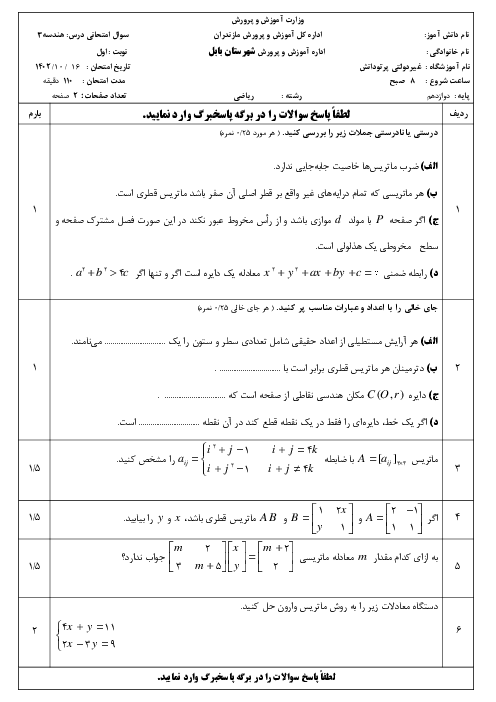
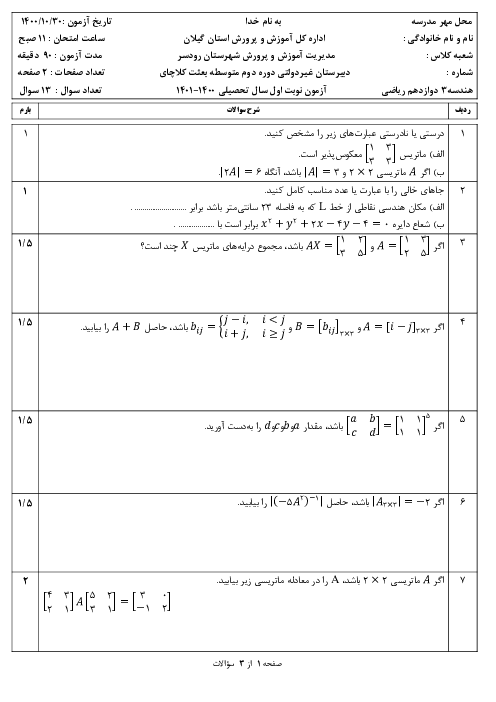
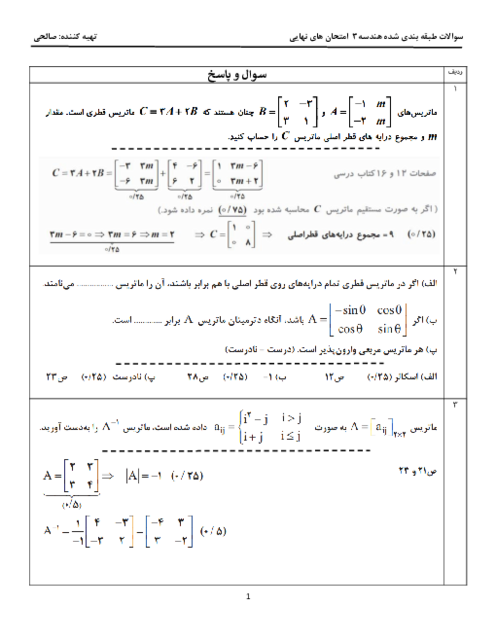
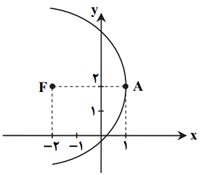
خط هادی و معادلهٔ سهمی با رأس $A(1,2)$ و کانون $F(-2,2)$ کدام است؟
1 )
$x=4$ و ${{y}^{2}}-4y-12x=8$
2 )
$x=-5$ و ${{y}^{2}}-4y-12x=8$
$x=4$ و ${{y}^{2}}-4y+12x=8$
4 )
$x=-5$ و ${{y}^{2}}-4y+12x=8$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...