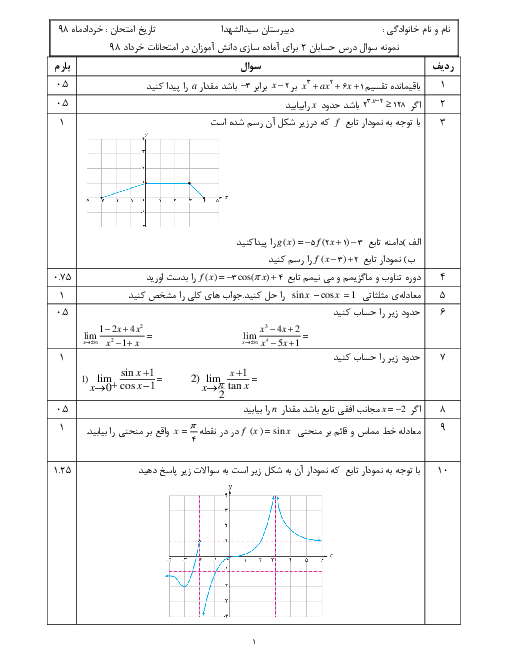
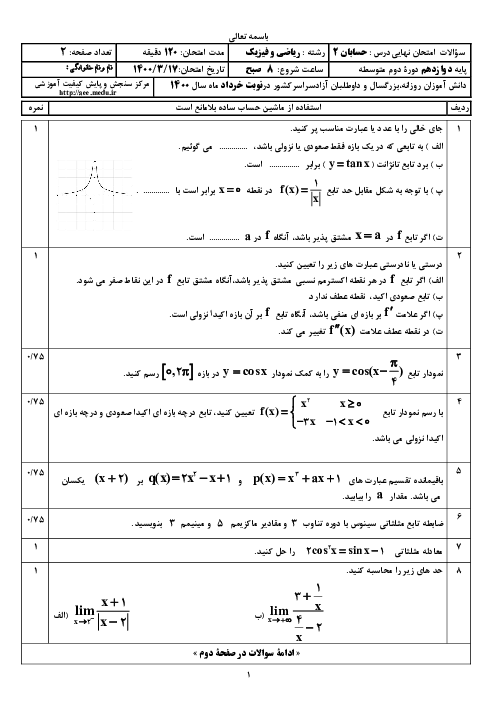
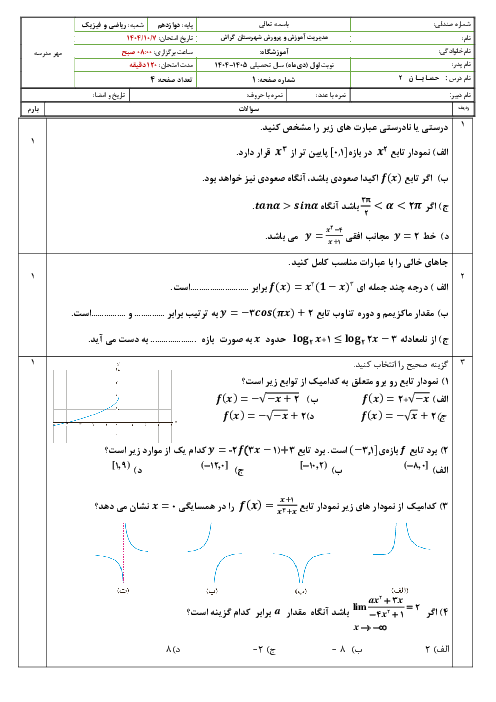
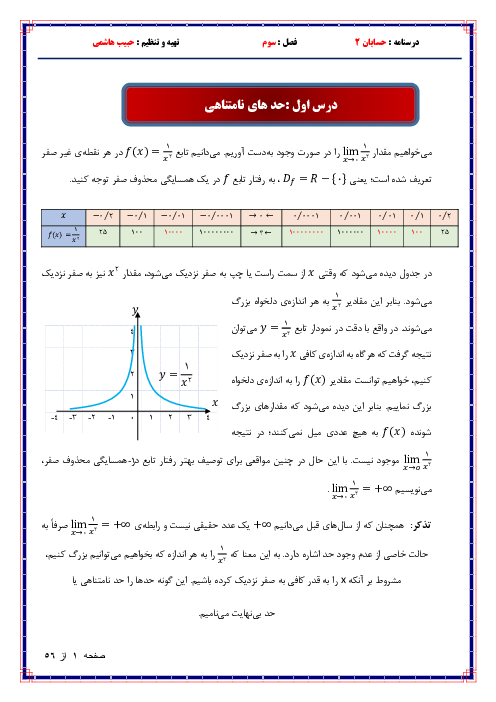
درس 2: تابع درجه سوم، توابع یکنوا و بخش‌پذیری و تقسیم
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
تابع $f(x)={{x}^{3}}+3{{x}^{2}}+ax+b$ در سه نقطه محور طول‌ها را قطع می‌کند. اگر حاصل ضرب طول این نقاط $+3$ و $f(2)=15$ باشد، $a$ کدام است؟
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...