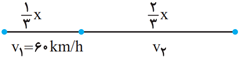در اينجا متحرک روی يک خط راست، $\frac{1}{3}x$ را با سرعت ثابت $60km/h$ و باقی مسير $(\frac{2}{3}x)$ را با سرعت متغيری بين 60 و 90 كيلومتر بر ساعت طی می‌كند. 

${{v}_{av}}=\frac{\Delta {{x}_{1}}+\Delta {{x}_{2}}}{{{t}_{1}}+{{t}_{2}}}=\frac{\frac{1}{3}x+\frac{2}{3}x}{\frac{x}{\frac{3}{60}+}\frac{2x}{\frac{3}{{{v}_{2}}}}}=\frac{x}{\frac{x}{180}+\frac{2x}{3{{v}_{2}}}}=\frac{x}{\frac{x{{v}_{2}}+120x}{180{{v}_{2}}}}=\frac{180{{v}_{2}}x}{x({{v}_{2}}+120)}=\frac{180{{v}_{2}}}{{{v}_{2}}+120}$

$\Rightarrow {{v}_{av}}=\frac{180{{v}_{2}}}{{{v}_{2}}+120}$

اكنون دو حد بالا و پايين سرعت در مرحلهٔ دوم را در اين رابطه قرار می‌دهيم تا حدود سرعت متوسط كل به‌دست آيد. چون سرعت متوسط در مرحلهٔ اول $60km/h$ است، بنابراين اگر سرعت متوسط در قسمت دوم نيز ${{v}_{2}}=60km/h$ باشد، ${{v}_{av}}$ کل نیز $60km/h$ خواهد بود.

حال حد بالا یعنی ${{v}_{2}}=90km/h$ را قرار می‌دهیم:

${{v}_{2}}=90km/h\Rightarrow {{v}_{av}}=\frac{180\times 90}{210}=\frac{540}{7}\simeq 77/1km/h$

ملاحظه می‌شود سرعت متوسط بايد بين 60 و 77/1 برحسب $km/h$ باشد كه در گزينهٔ «2» يعنی $70km/h$ اين شرايط برقرار است.