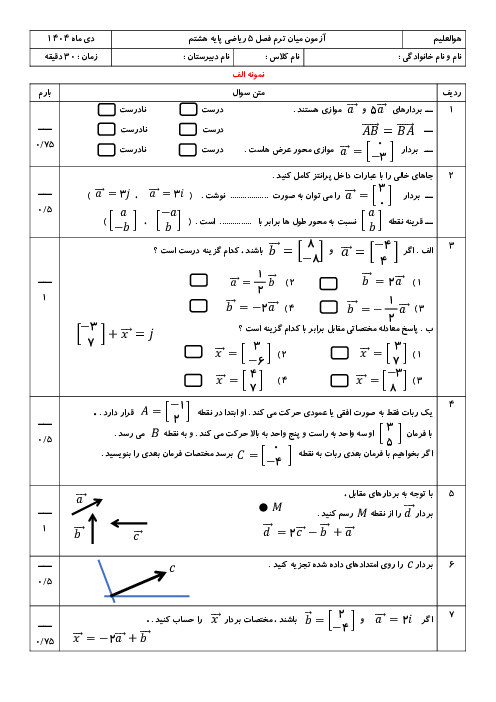
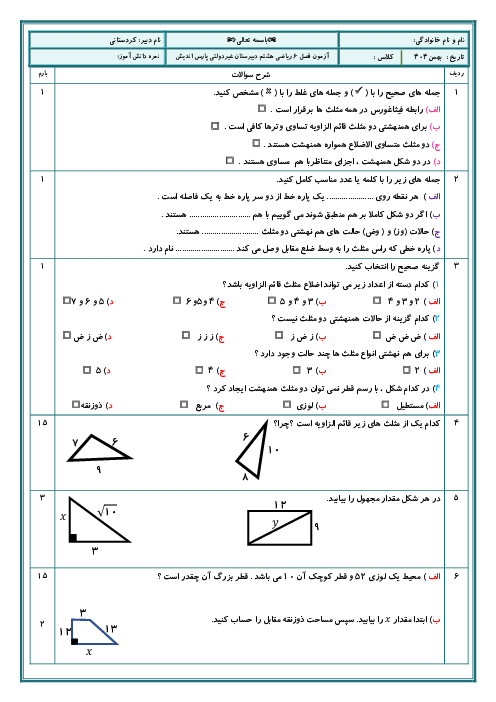
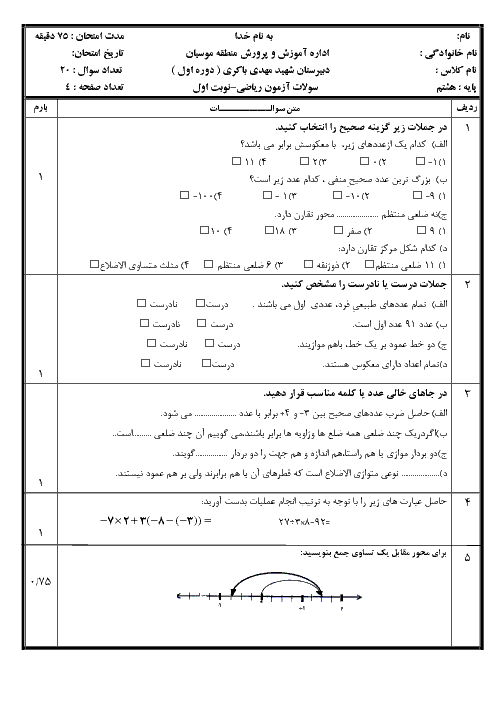
صورت سؤال:
می‌خواهیم با استفاده از دو نوع چندضلعی منتظم، یک صفحه را طوری کاشی‌کاری کنیم که فضای خالی باقی نماند. منظور از «منتظم» یعنی تمام اضلاع و زوایا برابر باشند.

اصل علمی:
برای اینکه چندضلعی‌ها بدون فاصله کنار هم قرار بگیرند و صفحه‌ای را کامل پر کنند (کاشی‌کاری منتظم)، زاویه داخلی‌شان باید طوری باشد که مجموعشان در یک نقطه برابر 360 درجه شود.

گزینه 1: مربع و مستطیل

مربع: چندضلعی منتظم است (4 ضلع، زاویه داخلی 90 درجه)

مستطیل: اضلاع مقابل برابرند اما زوایا 90 درجه‌اند و اضلاع هم‌طول نیستند → منتظم نیست

اگرچه مربع و مستطیل می‌توانند صفحه را پر کنند، اما چون مستطیل منتظم نیست ⇒ ❌ نادرست

گزینه 2: پنج‌ضلعی منتظم و مربع

پنج‌ضلعی منتظم: زاویه داخلی ≈ 108 درجه

مربع: زاویه داخلی 90 درجه

مجموع زاویه‌ها در اطراف یک نقطه باید 360 درجه شود، اما با این ترکیب امکان‌پذیر نیست.

همچنین، طبق اصول tiling، پنج‌ضلعی منتظم به‌تنهایی یا در ترکیب با مربع، صفحه را نمی‌پوشاند ⇒ ❌ نادرست

گزینه 3: لوزی و هشت‌ضلعی منتظم

هشت‌ضلعی منتظم: زاویه داخلی 135 درجه

لوزی: اگرچه همه اضلاع برابرند، اما زوایا برابر نیستند → لوزی منتظم نیست

پس استفاده از لوزی، شرط «چندضلعی منتظم» را نقض می‌کند ⇒ ❌ نادرست

گزینه 4: سه‌ضلعی منتظم و دوازده‌ضلعی منتظم

مثلث منتظم: زاویه داخلی 60 درجه

دوازده‌ضلعی منتظم: زاویه داخلی 150 درجه

سه عدد 150 + 60 + 150 = 360 → می‌توان آن‌ها را کنار هم قرار داد و بدون فضای خالی صفحه را پوشاند.

این ترکیب در کاشی‌کاری‌های نیمه‌منتظم (آرشمیدسی) به‌کار رفته و معتبر است ⇒ ✅ درست

نتیجه نهایی:

✅ پاسخ صحیح: گزینه 4
زیرا تنها ترکیبی از دو چندضلعی منتظم است که بدون فضای خالی صفحه را می‌پوشاند.