نمودار مكان – زمان نوسانگری كه بر روی محور نوسان می‌كند، مطابق شكل زير است. بردار شتاب نوسانگر در لحظۀ برحسب كدام است؟ | فیزیک (3) ریاضی دوازدهم شماره 82446

گاما رو نصب کن!

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

گام به گام نوبت اول کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نمونه سوال تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم گزارش کارورزی

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

قسمت 2: حرکت هماهنگ ساده فیزیک (3) ریاضی دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

نمودار مكان – زمان نوسانگری كه بر روی محور $x$ نوسان می‌كند، مطابق شكل زير است. بردار شتاب نوسانگر در لحظۀ ${{t}_{1}}$ برحسب $\frac{cm}{{{s}^{2}}}$ كدام است؟ $\left( {{\pi }^{2}}=10 \right)$

1 )

$40\overrightarrow{i}$

2 )

$-40\overrightarrow{i}$

3 )

$20\overrightarrow{i}$

4 )

$-20\overrightarrow{i}$

نمایش پاسخ

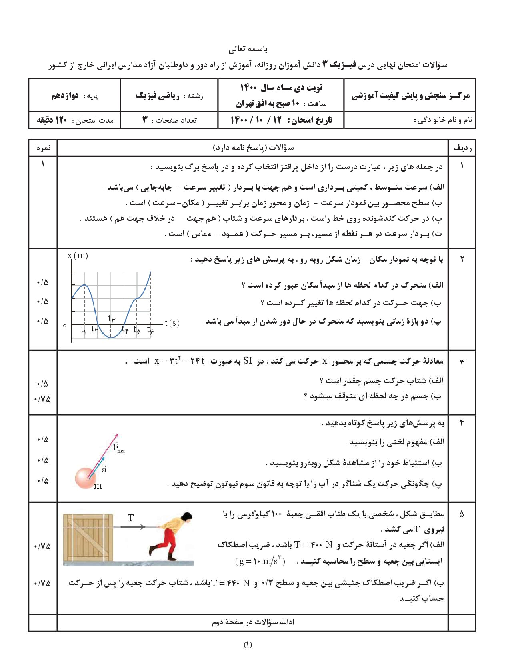
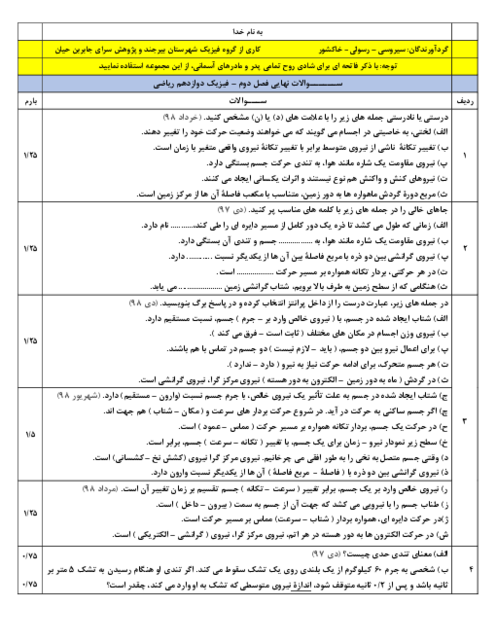
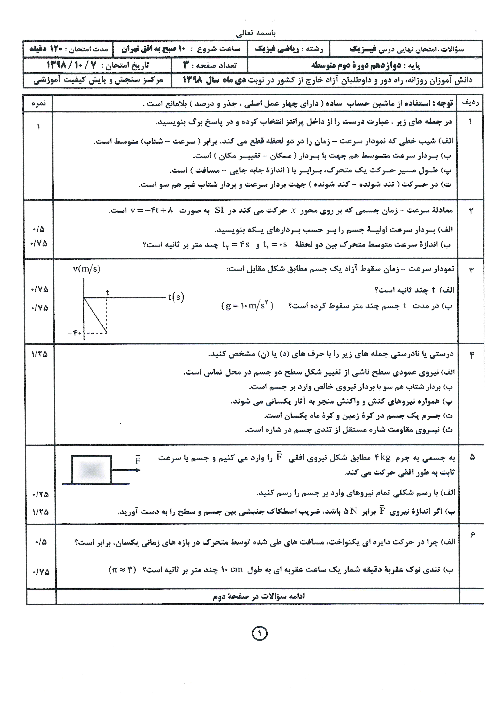
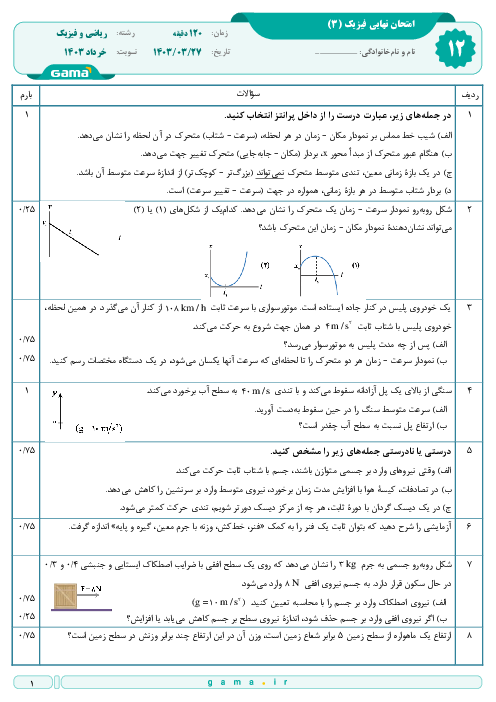
ابتدا دورۀ تناوب نوسانگر را محاسبه می‌كنيم، داريم:

$T+\frac{T}{2}=\frac{3T}{2}=3s\Rightarrow T=2s$

بسامد زاويه‌ای برابر است با

$\omega =\frac{2\pi }{T}=\frac{2\pi }{2}=\pi \frac{rad}{s}$

شتاب نوسانگر در هر لحظه به‌صورت زير قابل محاسبه است، داريم:

$\begin{matrix} F=ma \\ F=-kx \\ \end{matrix}\left. \begin{matrix} {} \\ {} \\ \end{matrix} \right\}\Rightarrow ma=-kx\Rightarrow a=\frac{-k}{m}x=-{{\omega }^{2}}x$

در لحظۀ ${{t}_{1}}$ مکان نوسانگر برابر $\left( -2cm \right)$ است. بنابراین:

$a=-{{\omega }^{2}}x\xrightarrow[x=-2cm]{\omega =\pi \frac{rad}{s}}a=-{{\pi }^{2}}\times \left( -2 \right)=2{{\pi }^{2}}=20\frac{cm}{{{s}^{2}}}$

در نهایت چون در لحظۀ ${{t}_{1}}$ ، نوسانگر در مكانی منفی قرار دارد و در حال نزديك شدن به مبدأ نوسان است، بنابراين شتاب آن مثبت است و بردار شتاب به صورت $\overrightarrow{a}=+20\overrightarrow{i}\frac{cm}{{{s}^{2}}}$ می‌باشد.

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده