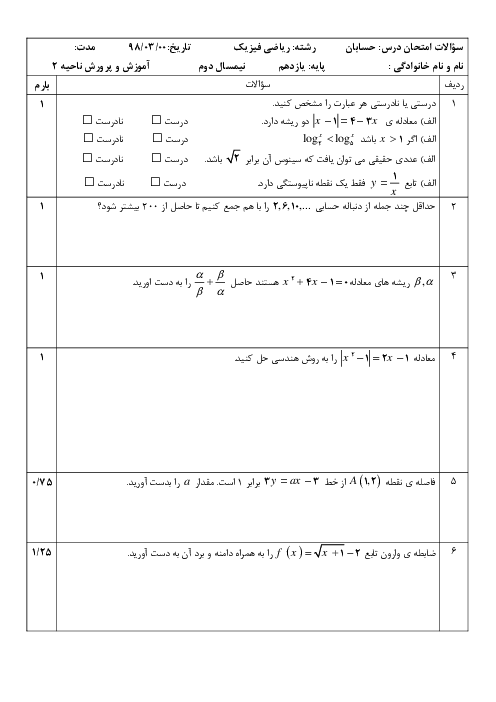
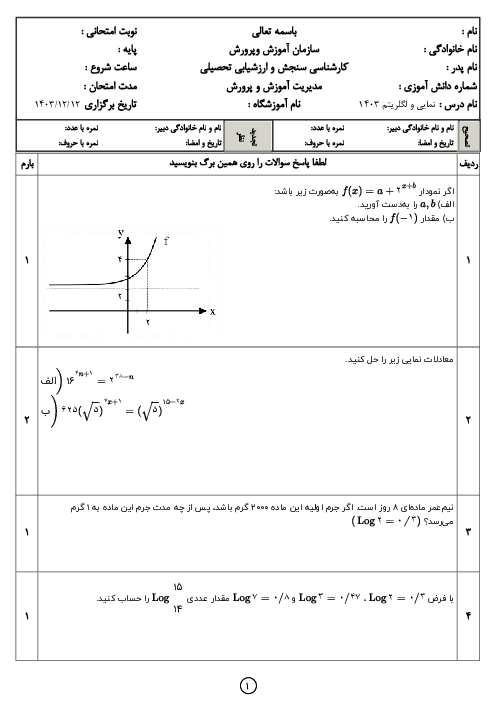
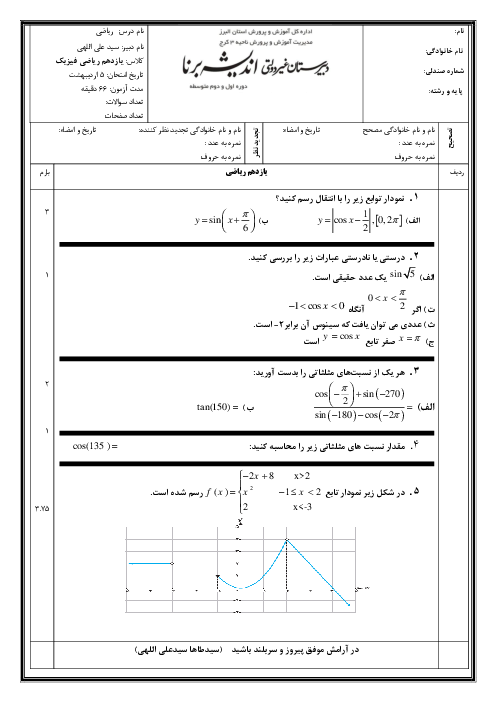
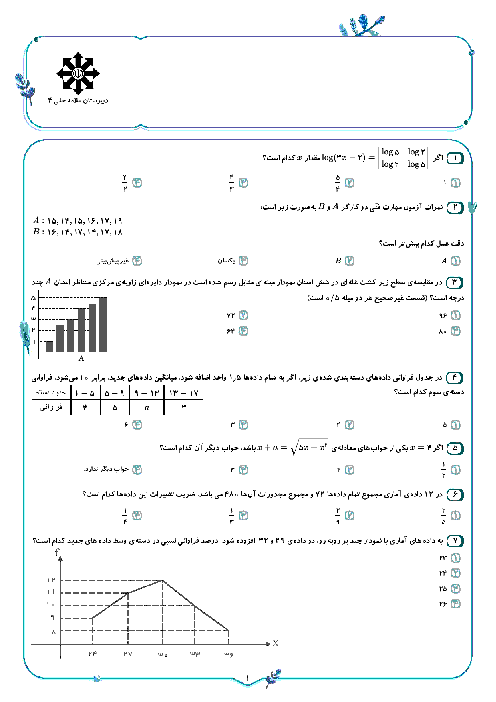
درس 4: روابط مثلثاتی مجموع و تفاضل زوایا
حسابان (1)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
حاصل عبارت $A=\sin x\cos x({{\cos }^{4}}x-{{\sin }^{4}}x)$ بهازای $x=\frac{\pi }{24}$ با کدام گزینه برابر است؟
1 )
$\frac{1}{4}$
$\frac{1}{8}$
3 )
$\frac{\sqrt{3}}{4}$
4 )
$\frac{\sqrt{3}}{8}$