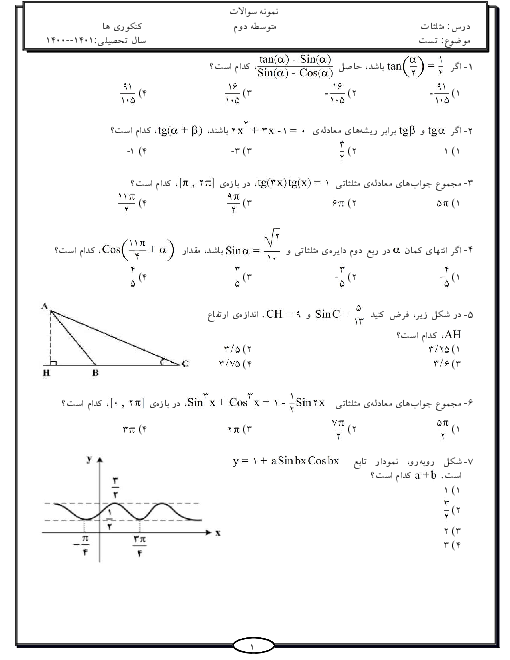
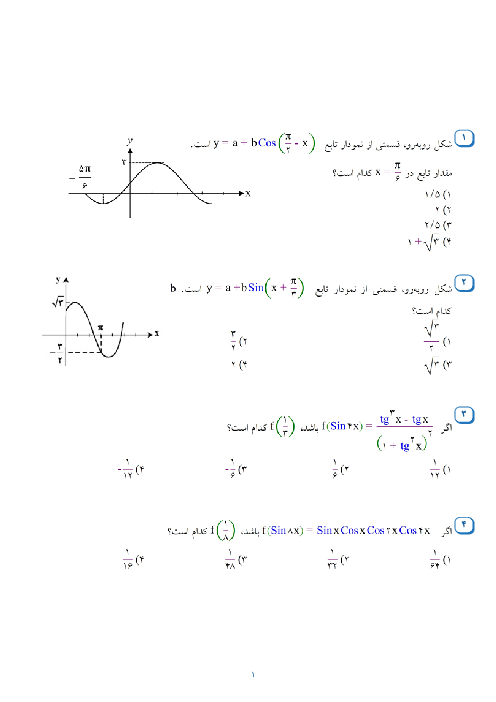
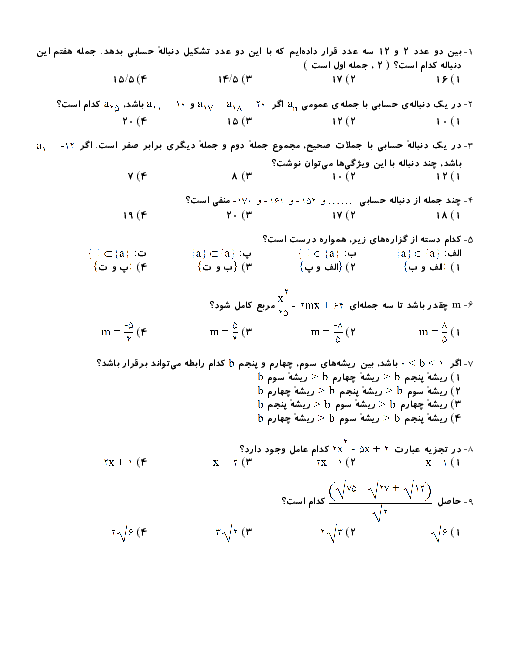برای اینکه تابع f در همه نقاط حد (و به تبع آن پیوسته) باشد، لازم است در ضابطه اول ضرایب ${\left[ x \right]}$ و ${\left[ { - x} \right]}$ برابر باشند:

$ \Rightarrow 1 - a = 3{a^2} - 1 \Rightarrow 3{a^2} + a - 2 = (a + 1)(3a - 2) = 0 \Rightarrow \begin{array}{*{20}{c}}
  {a =  - 1} \\ 
  {a = \frac{2}{3}} 
\end{array}$

به ازای ${a =  - 1}$ حد ضابطه بالا 2- اما حد ضابطه پایین صفر می‌شود که غیر قابل قبول است.

$\xrightarrow{{a = \frac{2}{3}}}f(x) = \left\{ \begin{gathered}
  \begin{array}{*{20}{c}}
  {\frac{1}{3}\left( {\left[ x \right] + \left[ { - x} \right]} \right)}&{x \notin \mathbb{Z}} 
\end{array} \hfill \\
  \begin{array}{*{20}{c}}
  {b\sin \frac{{3\pi }}{2} =  - b}&{x \in \mathbb{Z}} 
\end{array} \hfill \\ 
\end{gathered}  \right.$

در x های ناصحیح، حد تابع $ - \frac{1}{3}$ است، سپس داریم:

$ - b =  - \frac{1}{3} \Rightarrow b = \frac{1}{3}$
$ \Rightarrow \frac{a}{b} = 2$