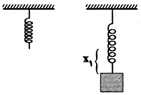
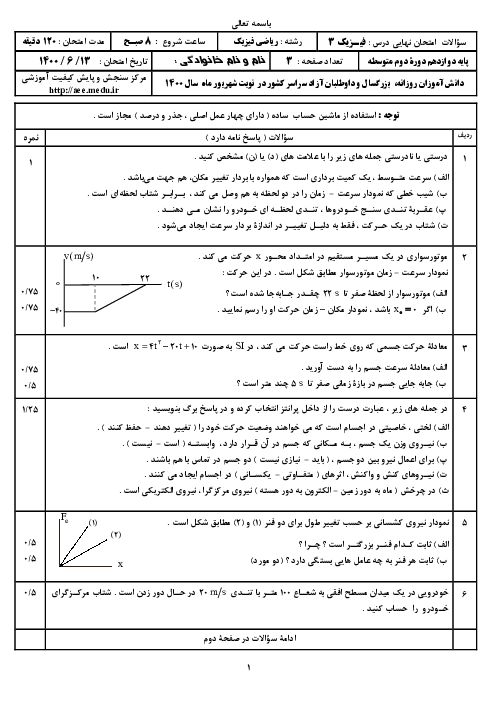
فنری به ضریب سختی به صورت قائم از سقفی آویزان است. وزنه‌ای به جرم را به آن متصل کرده و رها می‌کنیم تا سیستم وزنه و فنر به تعادل برسد. حال وزنه را از حالت تعادل… | فیزیک (3) ریاضی دوازدهم شماره 74484

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

قسمت 3: حرکت با شتاب ثابت فیزیک (3) ریاضی دوازدهم دوره دوم متوسطه- نظری علوم ریاضی درسنامه آموزشی این مبحث

فنری به ضریب سختی $100\frac{N}{m}$ به صورت قائم از سقفی آویزان است. وزنه‌ای به جرم $2kg$ را به آن متصل کرده و رها می‌کنیم تا سیستم وزنه و فنر به تعادل برسد. حال وزنه را $5cm$ از حالت تعادل جدید به پایین می‌کشیم و سپس رها می‌کنیم. شتاب حرکت وزنه بلافاصله پس از رها شدن چند متر بر مجذور ثانیه است؟

1 )

2 )

7/5

3 )

2/5

4 )

نمایش پاسخ

هنگامی که وزنه به فنر متصل می‌شود، طول فنر افزایش می‌یابد. حال افزایش طول فنر را ${{x}_{1}}$ در نظر می‌گیریم. چون فنر در حال تعادل هیچ شتابی ندارد، طبق قانون دوم نیوتون می‌توان نوشت:

$\sum{F=0}\Rightarrow mg-k{{x}_{1}}=0\Rightarrow mg=k{{x}_{1}}$

حال وزنه را توسط نیرویی می‌کشیم، طول فنر به اندازه‌ی ${{x}_{2}}$ افزایش می‌یابد، بنابراین:

$\sum{F}=ma\Rightarrow F-mg=ma\Rightarrow k({{x}_{1}}+{{x}_{2}})-mg=ma$

$\Rightarrow k{{x}_{1}}+k{{x}_{2}}-k{{x}_{1}}=ma\Rightarrow k{{x}_{2}}=ma$

$\Rightarrow a=\frac{k{{x}_{2}}}{m}=\frac{100\times 5\times {{10}^{-2}}}{2}=2/5\frac{m}{{{s}^{2}}}$