دو سيم هم‌جرم و هم‌جنس، يكی توپُر به شعاع و ديگری تو خالی به شعاع خارجی و شعاعی داخلی موجود می‌باشد. اگر مقاومت سيم توخالی برابر سيم توپُر باشد، نسبت به كدام…

موبایل / ایمیل

قوانین و مقررات را خواندم و می پذیرم.

لطفا کدی که به {{ identity }} ارسال شده است را وارد کنید.

کد فعال سازی :

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

لطفا برای حساب خود رمز عبور انتخاب کنید.

رمزعبور :

تکرار رمزعبور :

انصراف

موبایل / ایمیل

ورود | ثبت نام

لطفا کدی که برای شما ارسال شده است را وارد کنید.

کد فعال سازی :

ارسال مجدد کد فعال سازی {{ countDown }}

منتظر دریافت پیامک شما ...

برای حساب خود رمز عبور جدید انتخاب کنید.

رمزعبور :

تکرار رمزعبور :

انصراف

لطفا کمی صبر کنید ...

موبایل / ایمیل

رمزعبور

رمز عبور خود را فراموش کردید؟ بازیابی کنید.

هنوز عضو نشده اید؟ ثبت نام کنید.

انصراف

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

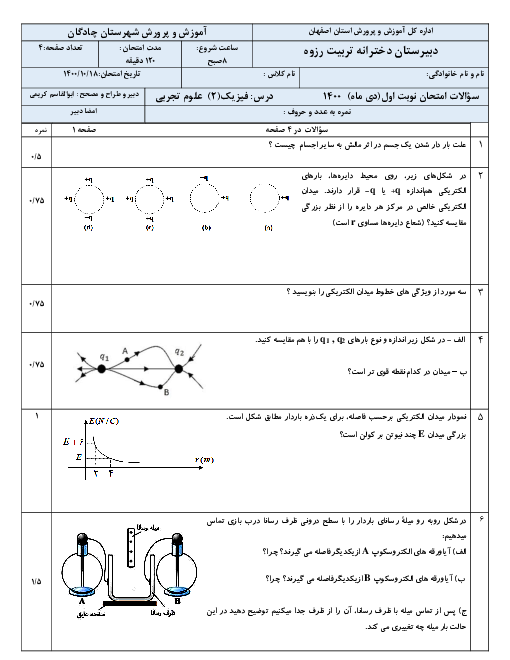
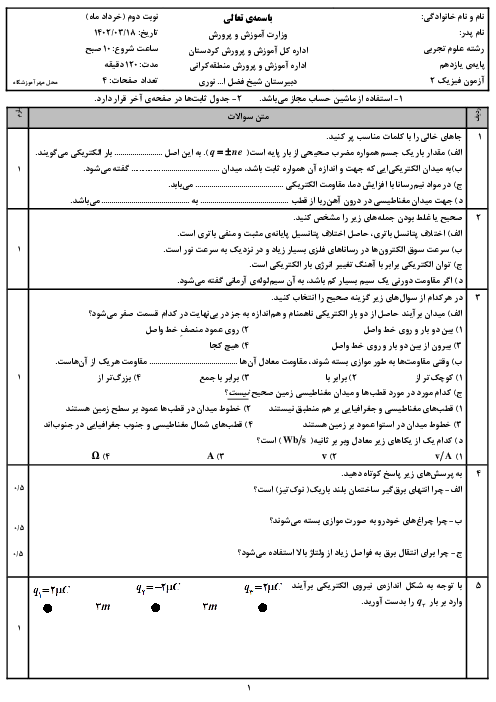
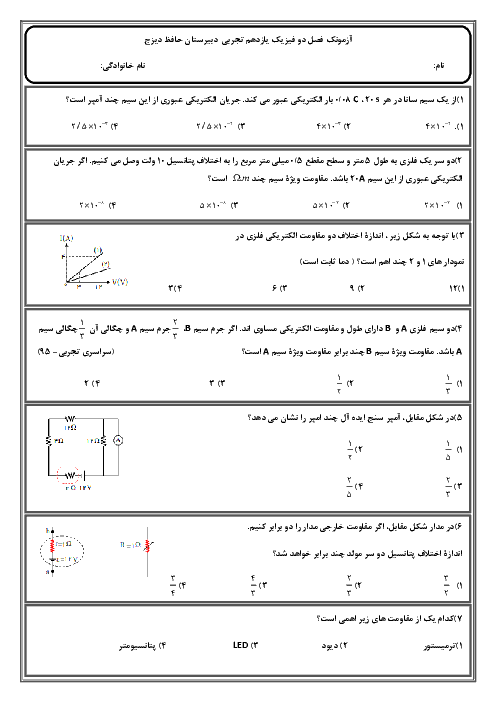
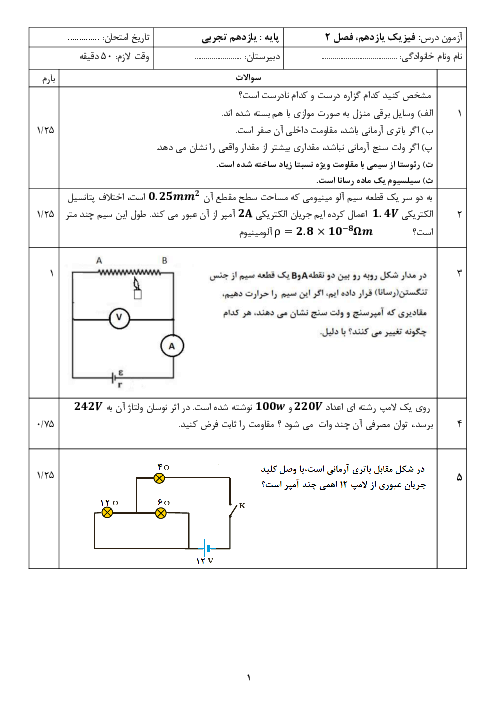
قسمت 3: عوامل مؤثر بر مقاومت الکتریکی فیزیک (2) یازدهم دوره دوم متوسطه- نظری علوم تجربی درسنامه آموزشی این مبحث

دو سيم هم‌جرم و هم‌جنس، يكی توپُر به شعاع $R$ و ديگری تو خالی به شعاع خارجی $R$ و شعاعی داخلی $r$ موجود می‌باشد. اگر مقاومت سيم توخالی $\frac{9}{4}$ برابر سيم توپُر باشد، نسبت $R$ به $r$ كدام است؟

1 )

$\frac{1}{3}$

2 )

3 )

$\sqrt{3}$

4 )

$\frac{\sqrt{3}}{3}$

نمایش پاسخ

سیم توپُر: $~\left. \begin{matrix} R \\ {{A}_{2}} \\ {{m}_{2}} \\ {{L}_{2}} \\ \end{matrix} \right\}$

سیم تو خالی: $\left. \begin{matrix} r,R \\ {{A}_{1}} \\ {{m}_{1}} \\ {{L}_{1}} \\ \end{matrix} \right\}$

جرم دو سيم برابر است، پس:

${{m}_{1}}={{m}_{2}}\Rightarrow {{{\rho }'}_{1}}{{V}_{1}}={{{\rho }'}_{2}}{{V}_{2}}\xrightarrow{{{{{\rho }'}}_{1}}={{{{\rho }'}}_{2}}}$

$\Rightarrow {{A}_{1}}{{L}_{1}}={{A}_{2}}{{L}_{2}}\Rightarrow \frac{{{L}_{1}}}{{{L}_{2}}}=\frac{{{A}_{2}}}{{{A}_{1}}}$

طبق رابطهٔ مقايسه‌ای برای مقاومت دو سيم رسانا داريم:

$\frac{{{R}_{1}}}{{{R}_{2}}}=\frac{{{\rho }_{1}}}{{{\rho }_{2}}}\times \frac{{{L}_{1}}}{{{L}_{2}}}\times \frac{{{A}_{2}}}{{{A}_{1}}}\xrightarrow[{{\rho }_{1}}={{\rho }_{2}}]{(1)}\frac{{{R}_{1}}}{{{R}_{2}}}={{(\frac{{{A}_{2}}}{{{A}_{1}}})}^{2}}$

$\Rightarrow \frac{9}{4}={{(\frac{\pi {{R}^{2}}}{\pi {{R}^{2}}-\pi {{r}^{2}}})}^{2}}\Rightarrow \frac{3}{2}=\frac{{{R}^{2}}}{{{R}^{2}}-{{r}^{2}}}$

$\Rightarrow 2{{R}^{2}}=3{{R}^{2}}-3{{r}^{2}}\Rightarrow {{R}^{2}}=3{{r}^{2}}\Rightarrow R=\sqrt{3}r$

گزارش خطا

پاسخ تشریحی :

تحلیل ویدئویی تست

با آلبوم تست

نمونه سوالات مرتبط