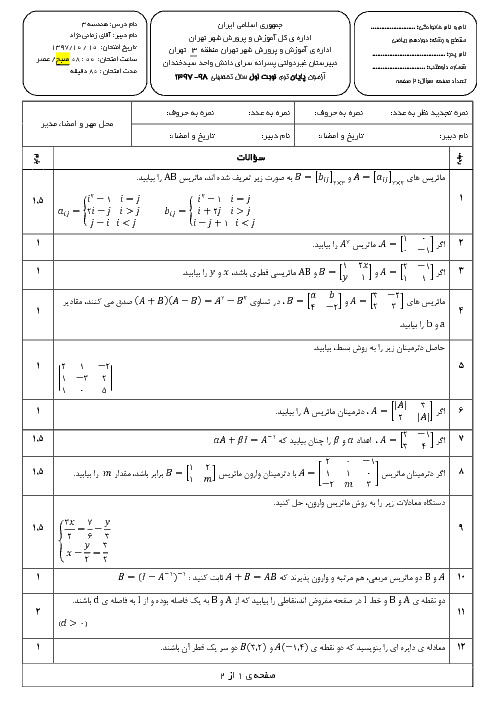
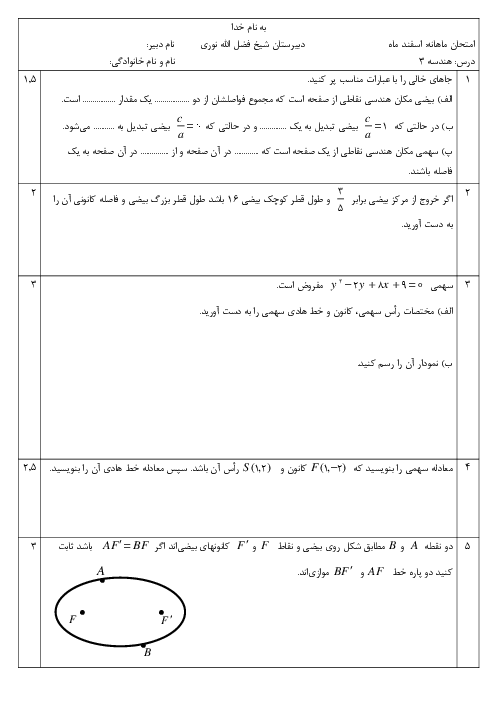
نكته: مكان هندسی نقاطی از صفحه كه از خط $d$ به فاصلۀ $r$  هستند، دو خط موازی $d$ در دو طرف آن و به فاصلۀ $r$ از آن است.

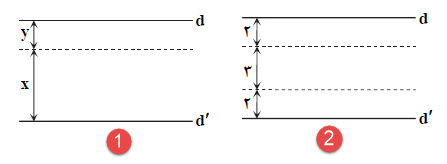
با توجه به اطلاعات مسئله، شكل (1) قابل رسم است:

با توجه به شكل داريم:

$\left\{ \begin{matrix}    x+y=7  \\    x-y=3  \\ \end{matrix} \right.\Rightarrow \left\{ \begin{matrix}    x=5  \\    y=2  \\  \end{matrix} \right.$

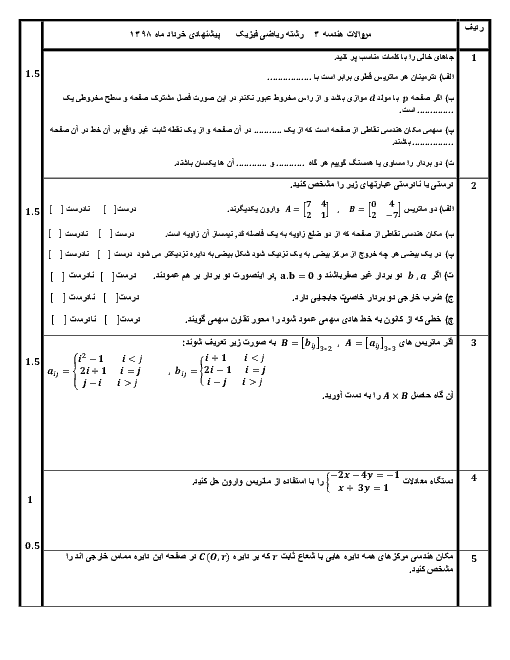
پس اين نقاط روی خط‌هايی قرار دارند كه به فاصله‌های ۵ و ۲ از ${d}',d$ هستند. یعنی مکان هندسی موردنظر دو خط موازی ${d}',d$ است.

دقت كنيد كه اگر خطوط موردنظر بين ${d}',d$ نباشد، قدرمطلق تفاضل فاصله‌ها برابر 3 نمی‌شود. به همین دليل آن‌ها را بين دو خط در نظر گرفتيم. (شکل 2)