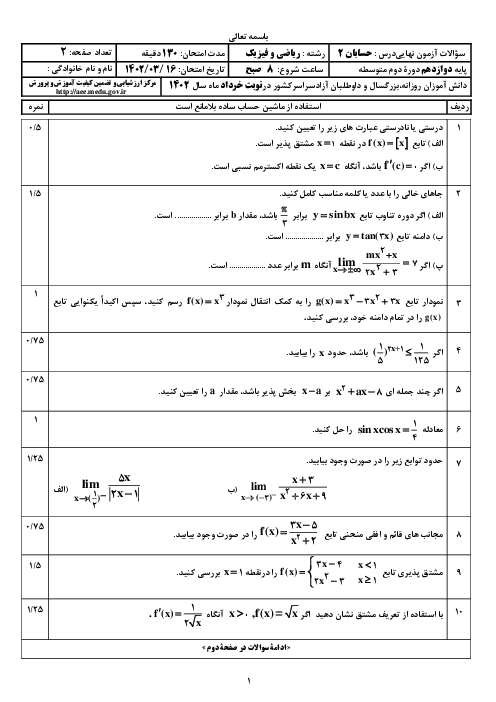
یک نقطه بر روی منحنی $y=\sqrt{x}$ در حال حرکت است. در لحظه‌ای که از نقطه‌ی $(4,2)$ می‌گذرد، مؤلفه‌ی $x$ آن با سرعت $3\frac{cm}{s}$ تغییر می‌کند. در این لحظه فاصله‌ی بین نقطه ومبدأ مختصات با چه آهنگی برحسب $\frac{cm}{s}$ تغییر می‌کند؟
1 )
$\frac{27}{2\sqrt{5}}$
2 )
$\frac{25}{2\sqrt{5}}$
$\frac{27}{4\sqrt{5}}$
4 )
$\frac{25}{4\sqrt{5}}$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...