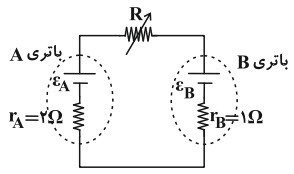
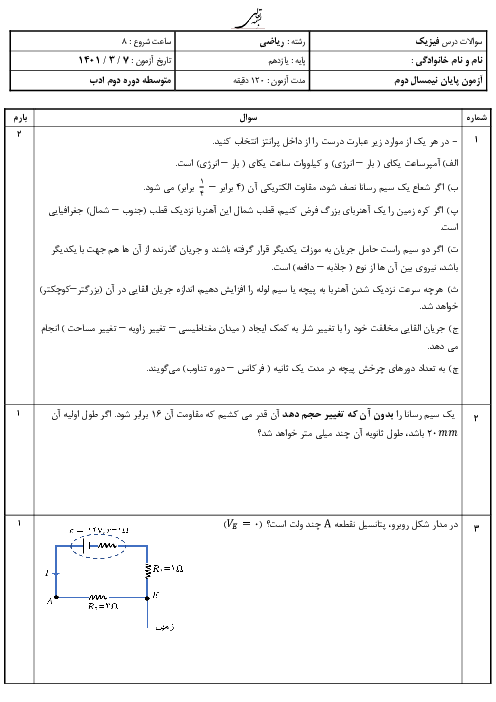
با توجه به جهت بسته‌شدن باتری‌ها، يكی از باتری‌ها به عنوان محركه و باتری ديگر به عنوان ضدمحركه است. اختلاف پتانسيل دو سر باتری محركه از رابطهٔ $V=\varepsilon -rI$ و اختلاف پتانسيل دو سر باتری ضدمحركه از رابطهٔ ${V}'={\varepsilon }'+{r}'I$ به دست می‌آید. از آن‌جا كه با افزايش مقاومت $R$ جريان عبوری از مدار كاهش می‌یابد، بنابراين:

 $\left. \begin{matrix} :V=\varepsilon -rI\xrightarrow{I\downarrow }V\uparrow   \\ :{V}'={\varepsilon }'+{r}'I\xrightarrow{I\downarrow }{V}'\downarrow   \\ \end{matrix} \right\}\Rightarrow ({{\varepsilon }_{B}}\gt {{\varepsilon }_{A}})$

چون در صورت سؤال ذكرشده كه اختلاف پتانسيل دو سر باتری $A$ كاهش يافته، پس باتری $B$ به عنوان محركه و باتری $A$ به عنوان ضدمحركه در مدار عمل می‌كند.

$I=\frac{{{\varepsilon }_{B}}-{{\varepsilon }_{A}}}{{{r}_{A}}+{{r}_{B}}+R}\xrightarrow[{{r}_{A}}=2\Omega ,{{r}_{B}}=1\Omega ]{R=1\Omega ,{R}'=3\Omega }$

$\left\{ \begin{matrix} I=\frac{{{\varepsilon }_{B}}-{{\varepsilon }_{A}}}{4}(*)  \\ {I}'=\frac{{{\varepsilon }_{B}}-{{\varepsilon }_{A}}}{6}(**)  \\ \end{matrix} \right.$

$\left\{ \begin{matrix} {{V}_{A}}={{\varepsilon }_{A}}+{{r}_{A}}I\xrightarrow{{{V}_{A}}-{{{{V}'}}_{A}}=2V}  \\ {{{{V}'}}_{A}}={{\varepsilon }_{A}}+{{r}_{A}}{I}'  \\ \end{matrix} \right.$

$({{\varepsilon }_{A}}+{{r}_{A}}I)-({{\varepsilon }_{A}}+{{r}_{A}}{I}')=2\xrightarrow{{{r}_{A}}=2\Omega }I-{I}'=1A$

$\xrightarrow{(*),(**)}({{\varepsilon }_{B}}-{{\varepsilon }_{A}})(\frac{1}{4}-\frac{1}{6})=1\Rightarrow {{\varepsilon }_{B}}-{{\varepsilon }_{A}}=12V$

$\xrightarrow[R=2\Omega ,{{r}_{A}}=2\Omega ,{{r}_{B}}=1\Omega ]{I=\frac{{{\varepsilon }_{B}}-{{\varepsilon }_{A}}}{{{r}_{A}}+{{r}_{B}}+R}}I=\frac{12}{5}=2/4A$

از آنجا كه ${{\varepsilon }_{B}}\gt {{\varepsilon }_{A}}$ است، بنابراين جريان در مدار پادساعتگرد است.