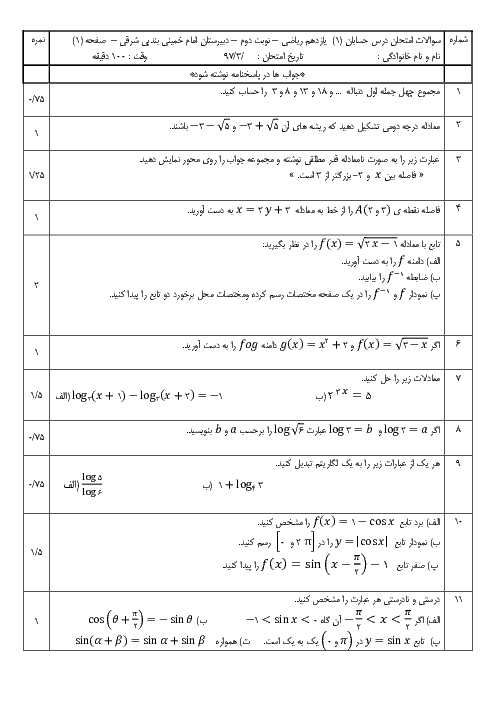
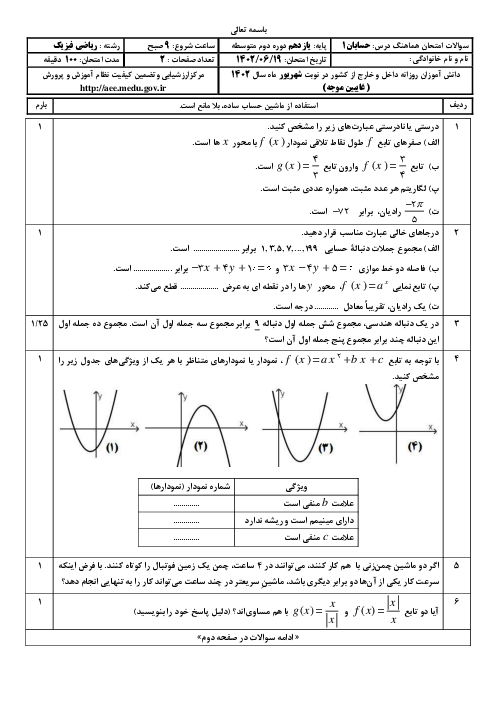
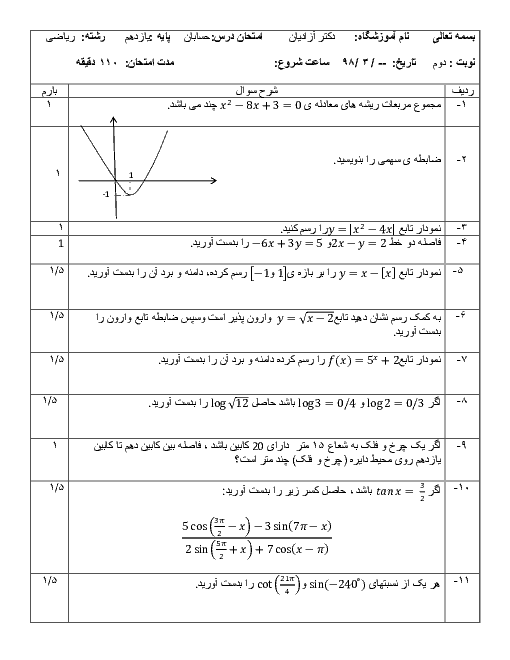
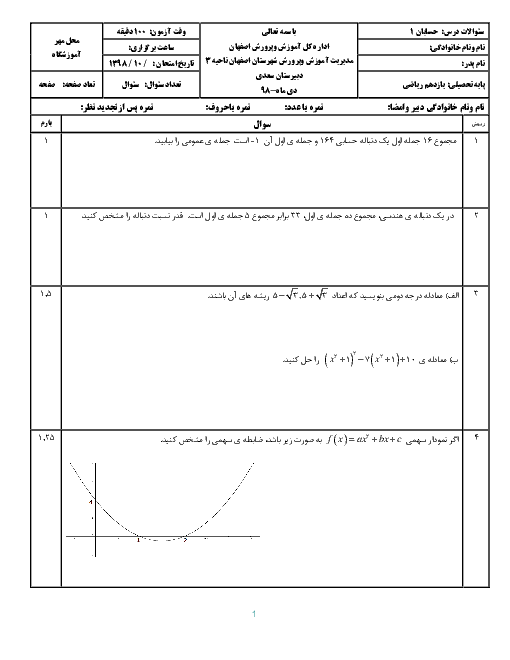
درس 1: مجموع جملات دنباله‌های حسابی و هندسی
حسابان (1)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
حاصل $A=\frac{{{a}^{9}}-1}{1+a+...+{{a}^{8}}}$ به ازای $a=\sqrt{2}+1$ کدام است؟
تحلیل ویدئویی تست
علیرضا زینی وند 
مهدی خلجی 
زهرا شیخ الاسلامی 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...