درس 2: تابع درجه سوم، توابع یکنوا و بخش‌پذیری و تقسیم
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
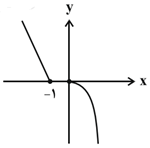
كدام‌يک از موارد زير در مورد تابع $f$ با ضابطهٔ $f(x)=\left\{ \begin{matrix} \begin{matrix} \left| x+1 \right| & ;x\le -1 \\ \end{matrix} \\ \begin{matrix} -{{x}^{2}} & ;x\ge 0 \\ \end{matrix} \\ \end{matrix} \right.$ درست است؟
1 )
صعودی است ولی اكيداً صعودی نيست.
2 )
اکیداً صعودی است.
نزولی است ولی اكيداً نزولی نيست.
4 )
اکیداً نزولی است.
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...