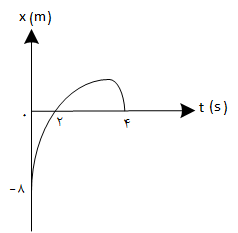
چون نمودار مکان - زمان متحرک سهمی است، بنابراین حرکت متحرک با شتاب ثابت است و می‌توان نوشت:

\[x=\frac{1}{2}a{{t}^{2}}+{{v}_{{}^\circ }}t+{{x}_{{}^\circ }}\xrightarrow{{{x}_{{}^\circ }}=-8m}x=\frac{1}{2}a{{t}^{2}}+{{v}_{{}^\circ }}t-8\] 

در نمودار می‌بینید که در دو لحظه‌ی ${{t}_{1}}=2s$ و ${{t}_{2}}=4s$ مکان متحرک $x=0$ است:

$\left\{ _{0=\frac{1}{2}a\times {{4}^{2}}+{{v}_{{}^\circ }}\times 4-8}^{0=\frac{1}{2}a\times {{2}^{2}}+{{v}_{{}^\circ }}\times 2-8}\Rightarrow \left\{ _{2a+{{v}_{{}^\circ }}=2}^{a+{{v}_{{}^\circ }}=4}\Rightarrow \left\{ _{{{v}_{{}^\circ }}=+6\frac{m}{s}}^{a=-2\frac{m}{{{s}^{2}}}} \right. \right. \right.$ 

حالا لحظه‌ و مکان تغییر جهت حرکت متحرک را پیدا می‌کنیم:

$_{{t}'=3s\Rightarrow {x}'=\frac{1}{2}a{{{{t}'}}^{2}}+{{v}_{{}^\circ }}{t}'+{{x}_{{}^\circ }}=\frac{1}{2}\times (-2)\times {{3}^{2}}+6\times 3-8=+1m}^{v=at+{{v}_{{}^\circ }}\Rightarrow 0\Rightarrow -2{t}'+6\Rightarrow {t}'=3s}$ 

به کمک مسیر حرکت متحرک مسافت طی‌شده را در $4$ ثانیه‌ی اول حساب می‌کنیم: