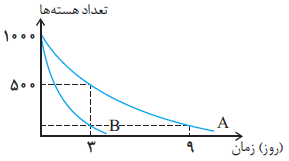
برای تعيين هسته‌های باقی‌مانده‌ی عنصر $B$ در يك مدت، بايد نيمه‌عمر آن را به دست آوریم.

طبق نمودار به راحتی درمی‌يابيم كه نيمه‌عمر عنصر $A$، $3$ روز است و تعداد هسته‌های باقی‌مانده‌ی دو عنصر $A$ و $B$ به‌ترتيب در زمان‌های ${{t}_{A}}=9\,\,(Rooz)$ و ${{t}_{B}}=3\,\,(Rooz)$ برابر می‌شوند.

بنابراين می‌توان با استفاده از رابطه‌ی هسته‌های باقی‌مانده $N=\frac{{{N}_{{}^\circ }}}{{{2}^{n}}}$، نیمه‌عمر عنصر $B$ را محاسبه کرد.

${{N}_{A}}={{N}_{B}}\xrightarrow{N=\frac{{{N}_{{}^\circ }}}{{{2}^{n}}}}\frac{{{N}_{{}^\circ }}}{{{2}^{n}}A}=\frac{{{N}_{{}^\circ }}}{{{2}^{n}}B}\xrightarrow{{{n}_{A}}=\frac{{{t}_{A}}}{{{T}_{\frac{1}{2}}}}=\frac{9}{3}=3}\frac{1}{{{2}^{3}}}=\frac{1}{{{2}^{{{n}_{B}}}}}\Rightarrow {{n}_{B}}=3$ 

از طرفی طبق رابطه‌ی $n=\frac{t}{{{T}_{\frac{1}{2}}}}$ می‌توانيم نيمه‌عمر $B$ را محاسبه کنیم.

${{n}_{B}}=\frac{{{t}_{B}}}{{{T}_{\frac{1}{2}}}}\xrightarrow{{{n}_{B}}=3,{{t}_{B}}=3\,\,(Rooz)}{{T}_{\frac{1}{2}(B)}}=1\,(Rooz)\,$ 

حال دوباره از رابطه‌ی $N=\frac{{{N}_{{}^\circ }}}{{{2}^{n}}}$، استفاده كرده و هسته‌های فعال $B$ را محاسبه می‌کنیم:

${{N}_{B}}=\frac{{{N}_{{}^\circ }}}{{{2}^{{{n}_{B}}}}}\xrightarrow{{{N}_{B}}=\frac{1}{32}{{N}_{{}^\circ }}}{{2}^{{{n}_{B}}}}=32\Rightarrow {{n}_{B}}=5\xrightarrow{{{n}_{B}}=\frac{{{t}_{B}}}{{{T}_{\frac{1}{2}}}}}{{t}_{B}}=5\,\,(Rooz)$