اگر یک تابع باشد، مقادیر a و b را بیابید. | ریاضی و آمار (2) یازدهم شماره 378645

گاما رو نصب کن!

درحال دریافت اطلاعات ...

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت دوم نمونه سوال گام به گام سوالات امتحان نهایی کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نوبت اول تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

** فصل 2: تابع ریاضی و آمار (2) یازدهم دوره دوم متوسطه- نظری ادبیات و علوم انسانی درسنامه آموزشی این مبحث

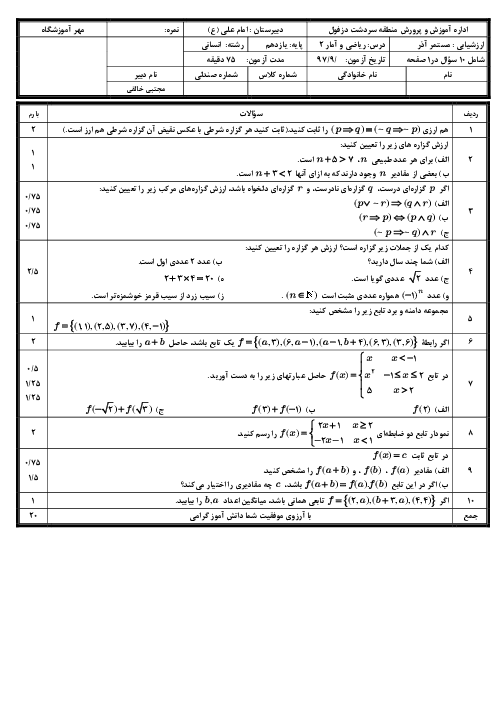
اگر $f(x) = \left\{ {\begin{array}{*{20}{c}} 3&{x \leqslant - 1} \\ {2ax + 1}&{ - 1 \lt x \leqslant 2} \\ {1 + b - {x^2}}&{2 \lt x} \end{array}} \right.$ یک تابع باشد، مقادیر a و b را بیابید.

نمایش پاسخ

باید به ازای مقدار x یک مقدار y به دست آید. بنابراین در نقطه $x = 2$ باید yها برابر باشند. یعنی:

$\eqalign{
& f( - 1) = 2a( - 1) + 1 = - 2a + 1 \cr
& f( - 1) = 3 \cr} $

بنابراین $ - 2a + 1$ باید برابر با 3 شود. پس:

$\eqalign{
& - 2a + 1 = 3 \to - 2a = 3 - 1 \to - 2a = 2 \to a = - 1 \cr
& f(2) = 2a(2) + 1 = 4a + 1 = 4( - 1) + 1 = - 4 + 1 = - 3 \cr
& f(2) = 1 + b - {2^2} = 1 + b - 4 = b - 3 \cr} $

بنابراین $b - 3$ باید برابر با 3- شود. پس:

$b - 3 = - 3 \to b = - 3 + 3 \to b = 0$

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده