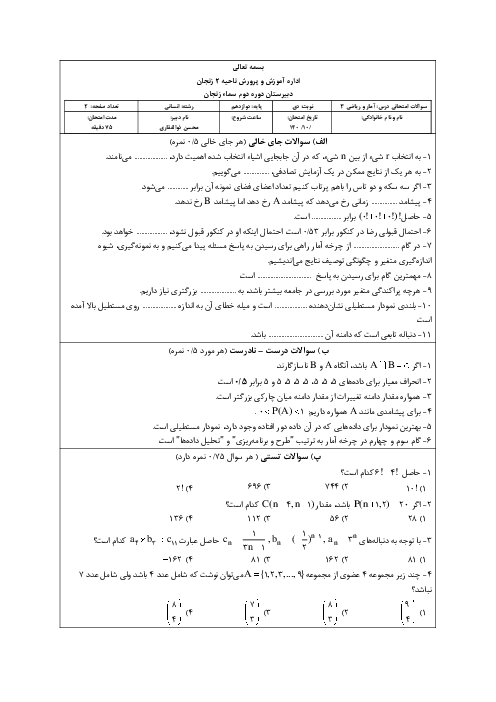
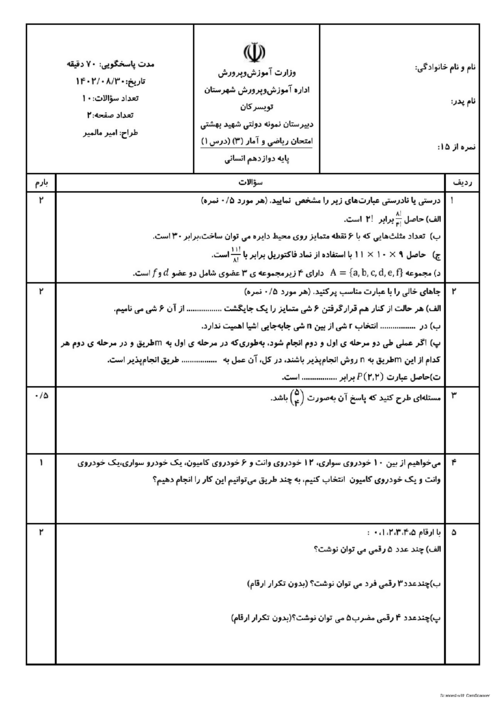
جملهٔ دوم = $24\Rightarrow {{a}_{2}}=24\Rightarrow {{a}_{1}}+d=24$

جملهٔ نهم = $-11\Rightarrow {{a}_{9}}=-11\Rightarrow {{a}_{1}}+8d=-11$

دو معادلهٔ بالا را در یک دستگاه حل می‌کنیم تا ${{a}_{1}}$ و $d$ به دست آیند.

$\begin{align}
& \left\{ \begin{matrix}
{{a}_{1}}+d=24\,\,\,\,\, \\
{{a}_{1}}+8d=-11 \\
\end{matrix}\,\, \right.\,\begin{matrix}
\xrightarrow{\times (-1)} \\
\xrightarrow{{}} \\
\end{matrix}\,\,\underline{\left\{ \begin{matrix}
-{{a}_{1}}-d=-24 \\
{{a}_{1}}+8d=-11 \\
\end{matrix} \right.\,\,}\,\oplus \\
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,7d=-35\Rightarrow d=-5 \\
\end{align}$

با جای‌گذاری $d=-5$ در معادلهٔ ${{a}_{1}}+d=24$، مقدار ${{a}_{1}}$ را حساب می‌کنیم:

${{a}_{1}}+(-5)=24\Rightarrow {{a}_{1}}=24+5\Rightarrow {{a}_{1}}=29$

چون سوال پرسیده جملهٔ چندم این دنباله $-56$ است، پس به جملهٔ عمومی دنباله نیاز داریم. با داشتن ${{a}_{1}}=29$ و $d=-5$، جملهٔ عمومی را می‌نویسیم:

${{a}_{n}}={{a}_{1}}+(n-1)d\Rightarrow {{a}_{n}}=29+(n-1)(-5)$

$\Rightarrow {{a}_{n}}=29-5n+5\Rightarrow {{a}_{n}}=-5n+34$

برای این‌که ببینیم جملهٔ چندم این دنباله $-56$ است، جای ${{a}_{n}}$، عدد $-56$ را قرار می‌دهیم تا $n$ به دست‌ آید:

${{a}_{n}}=-5n+34\Rightarrow -56=-5n+34\Rightarrow 5n=34+56$

$\Rightarrow 5n=90\Rightarrow n=\frac{90}{5}=18$

اگر جملات دوم و نهم یک دنبالهٔ حسابی به‌ترتیب $۲۴$ و $-۱۱$ باشند. جملهٔ چندم اینن دنباله برابر با $-۵۶$ است؟