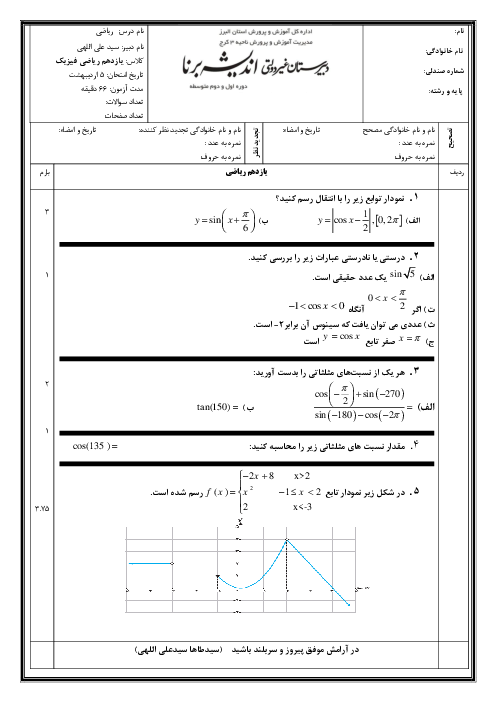
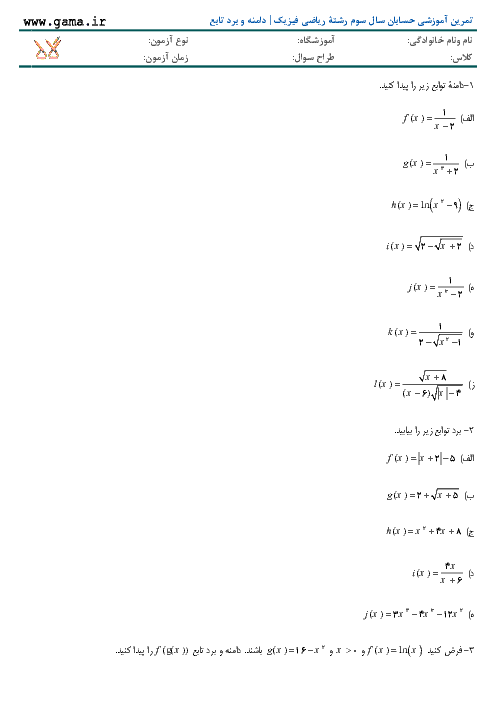1) $f(x)=\left\{ \begin{matrix} \frac{1}{{{x}^{2}}},x\ne 1  \\ 0,x=1  \\ \end{matrix} \right.$

در $x=1$ ناپیوسته است. $f(1)=0$ و $\Rightarrow \underset{x\to 1}{\mathop{\lim }}\,f(x)=\underset{x\to 1}{\mathop{\lim }}\,(\frac{1}{{{x}^{2}}})=1$

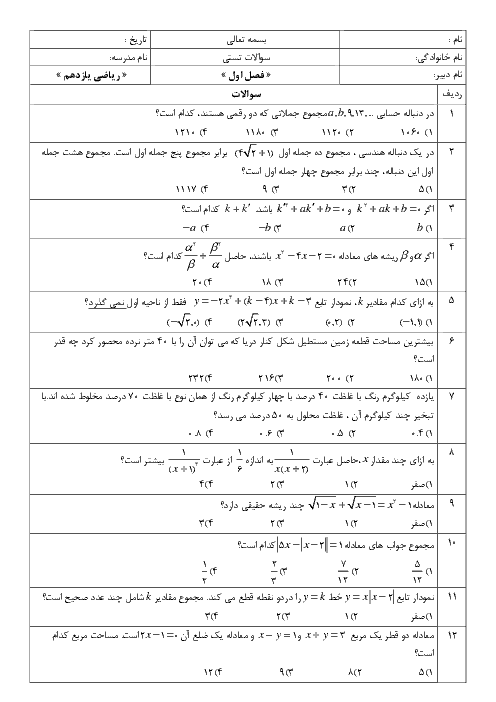
2) $f(x)=\left\{ \begin{matrix} \frac{{{x}^{3}}-x}{{{x}^{2}}-1},x\ne 1  \\ -1,x=1  \\ \end{matrix}\Rightarrow f(1)=-1,\underset{x\to 1}{\mathop{\lim }}\,f(x)= \right.\underset{x\to 1}{\mathop{\lim }}\,(\frac{{{x}^{3}}-x}{{{x}^{2}}-1})$

$=\underset{x\to 1}{\mathop{\lim }}\,\frac{x({{x}^{2}}-1)}{({{x}^{2}}-1)}=\underset{x\to 1}{\mathop{\lim }}\,(x)=1$

با توجه به این‌که مقادیر حد چپ و راست و مقدار تابع در نقطهٔ $x=1$ با هم برابر نیستند، تابع در این نقطه ناپیوسته است.

3) $f(x)=\left\{ \begin{matrix} {{x}^{2}}+1+\frac{\left| x-1 \right|}{x-1},x\ne 1  \\ 3,x=1  \\ \end{matrix} \right.$

$\Rightarrow \left\{ \begin{matrix} \underset{x\to {{1}^{+}}}{\mathop{\lim }}\,f(x)=\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,({{x}^{2}}+1+\frac{(x-1)}{(x-1)}=3  \\ f(1)=3  \\ \underset{x\to {{1}^{-}}}{\mathop{\lim }}\,f(x)=\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,({{x}^{2}}+1+\frac{-(x-1)}{(x-1)}=1  \\ \end{matrix} \right.$

اين تابع در نقطهٔ $x=1$ فقط پيوستگی راست دارد اما ناپيوسته است. 

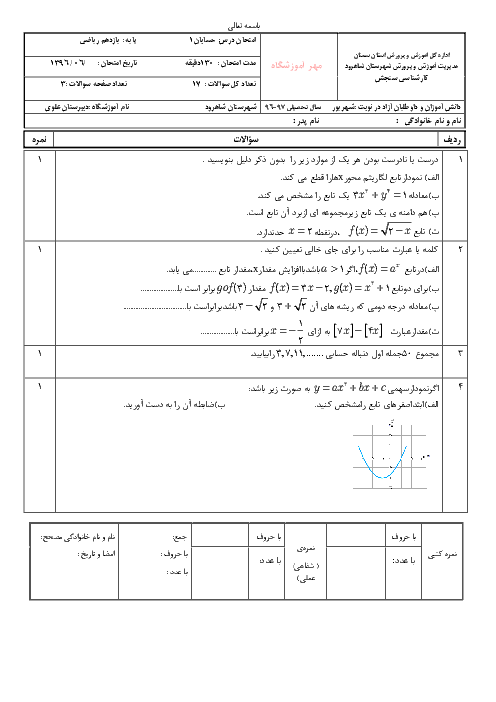
4) $f(x)=\left\{ \begin{matrix} \frac{-x+\left| x-2 \right|}{x-1},x\ne 1  \\ -2,x=1  \\ \end{matrix} \right.$

توجه کنید که:

$x\to {{1}^{+}}$ یا $x\to {{1}^{-}}$ $\Rightarrow x-2\lt 0$

$\Rightarrow \left\{ \begin{matrix} \underset{x\to 1}{\mathop{\lim }}\,f(x)=\underset{x\to 1}{\mathop{\lim }}\,(\frac{-x-(x-2)}{x-1})=\underset{x\to 1}{\mathop{\lim }}\,\frac{-2(x-1)}{x-1}=-2  \\ f(1)=-2  \\ \end{matrix} \right.$

بنابراين تابع گزينهٔ «4» در نقطهٔ $x=1$ پيوسته است.