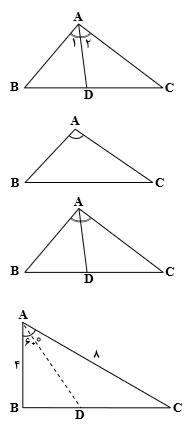
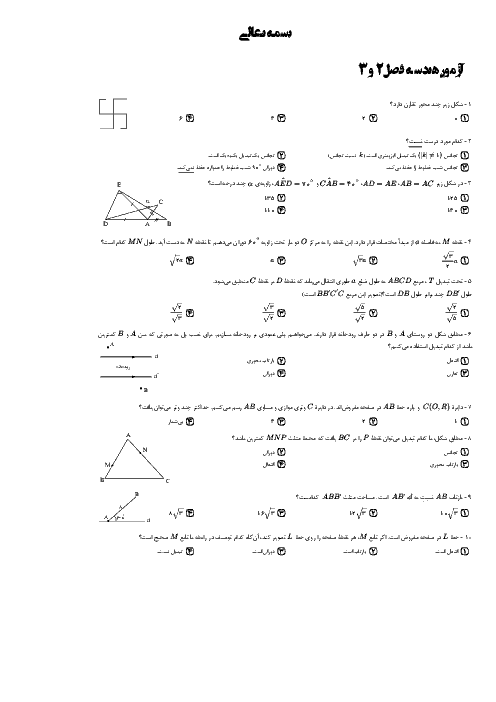
نکته (قضیهٔ نیمساز): در هر مثلث، نیمساز هر زاویهٔ داخلی، ضلع روبه‌رو به آن زاویه را به نسبت‌ اندازه‌های اضلاع آن زاویه تقسیم می‌کند.

${{\hat{A}}_{1}}={{\hat{A}}_{2}}\Rightarrow \frac{BD}{CD}=\frac{AB}{AC}$

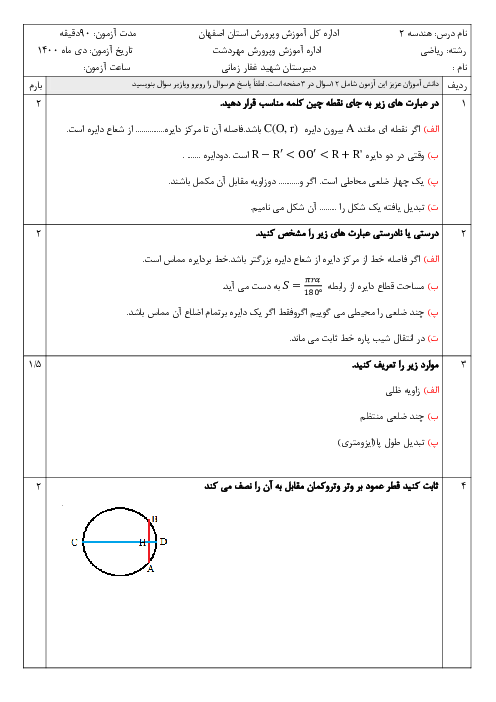
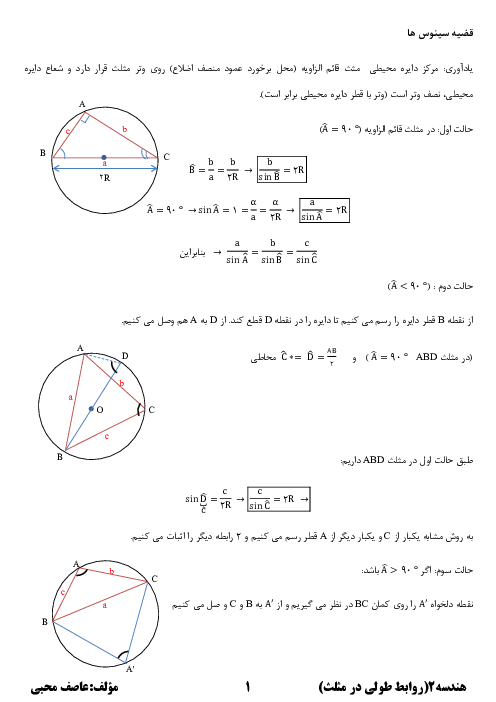
نکته (قضیهٔ کسینوس‌ها): در مثلث دلخواه $ABC$ داریم:

$B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}-2AB\times AC\times \operatorname{Cos}\hat{A}$

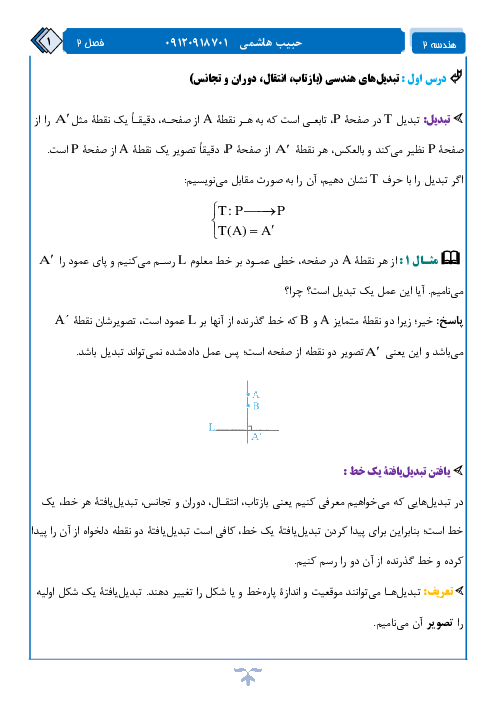
نکته: در مثلث دلخواه $ABC$ اگر $AD$  نیمساز زاویهٔ داخلی $A$ باشد، داریم:

$A{{D}^{2}}=AB\cdot AC-BD\cdot DC$

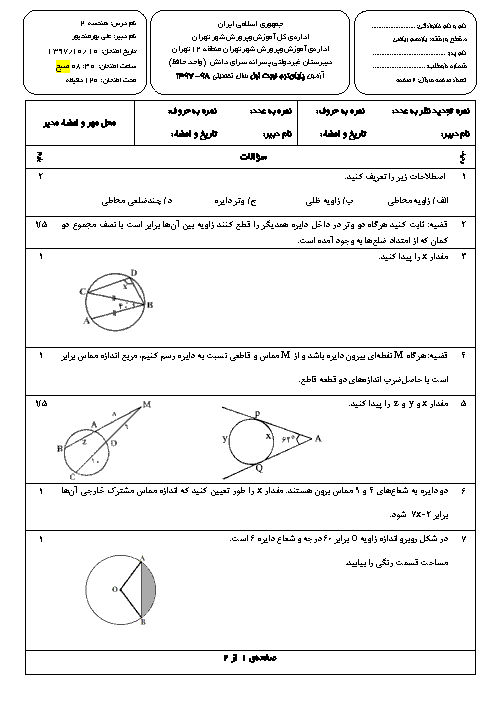
ابتدا با استفاده از قضیهٔ کسینوس‌ها، طول ضلع $BC$ را به‌دست می‌آوریم:

$B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}-2\times AB\times AC\times \operatorname{Cos}\,\hat{A}$

$B{{C}^{2}}={{4}^{2}}+{{8}^{2}}-2\times 4\times 8\times \frac{1}{2}\Rightarrow B{{C}^{2}}=48\Rightarrow BC=\sqrt{48}=4\sqrt{3}$

حال طول قطعاتی را که نیمساز $AD$ روی ضلع $BC$ ایجاد می‌کند، به‌دست می‌آوریم:

$\frac{BD}{CD}=\frac{AB}{AC}=\frac{4}{8}=\frac{1}{2}\to \frac{BD}{BC}=\frac{1}{3}\Rightarrow \frac{BD}{4\sqrt{3}}=\frac{1}{3}\Rightarrow BD=\frac{4}{3}\sqrt{3}$

$\Rightarrow CD=\frac{8}{3}\sqrt{3}$

اکنون طول نیمساز $AD$ را به‌دست می‌آوریم:

$A{{D}^{2}}=AB\times AC-BD\times CD\Rightarrow A{{D}^{2}}=4\times 8-\frac{4}{8}\sqrt{3}\times \frac{8}{3}\sqrt{3}\Rightarrow A{{D}^{2}}=\frac{64}{3}\Rightarrow AD=\frac{8}{\sqrt{3}}=\frac{8\sqrt{3}}{3}$