درس 2: تابع درجه سوم، توابع یکنوا و بخش‌پذیری و تقسیم
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
اگر $f=\left\{ \left( 1,2 \right),\left( -1,0 \right),\left( 0,\left[ a \right] \right) \right\}$ و $g\left( x \right)={{2}^{x}}$ باشند، به ازای چه مقادیری از $a$ تابع $f+g$ صعودی است؟ ($\left[ {} \right]$ ، علامت جزء صحیح است.)
1 )
$\left[ 0,3 \right]$
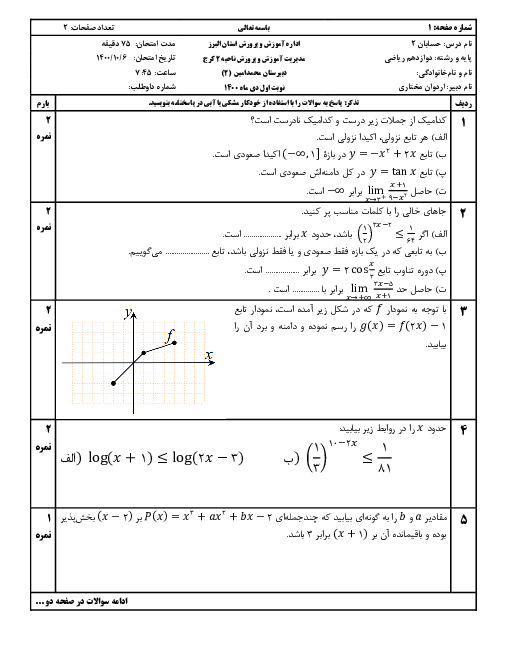
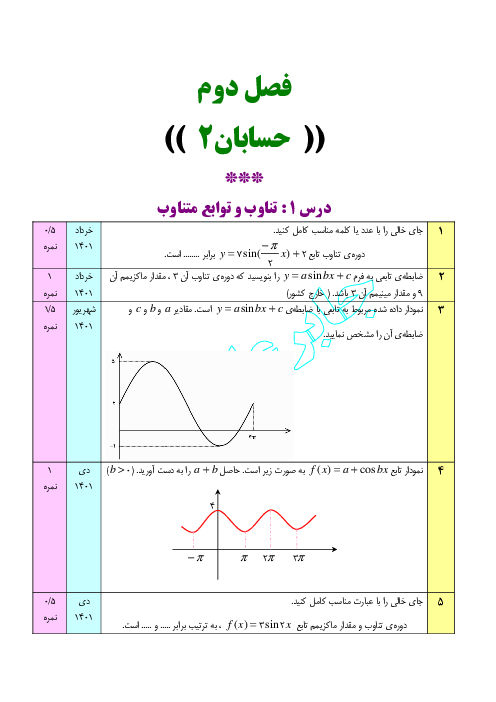
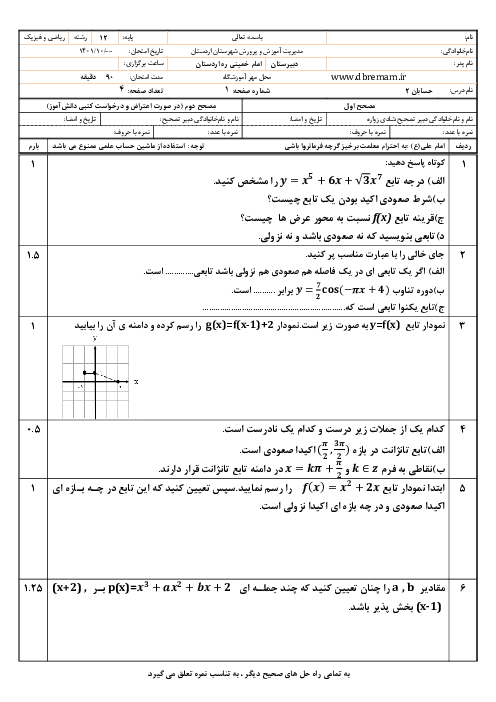
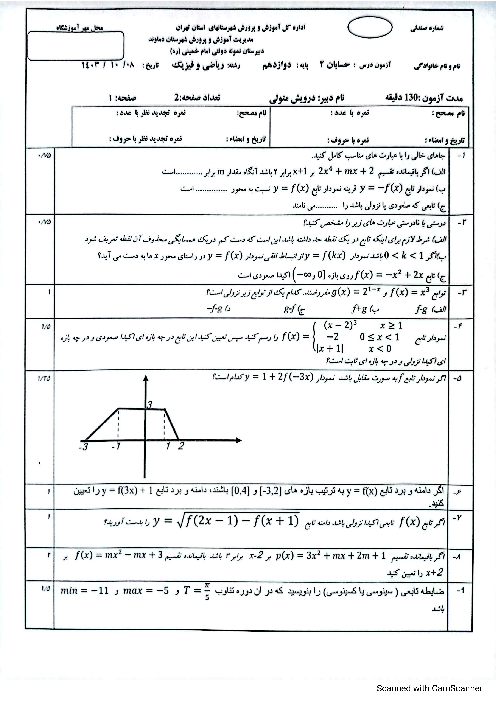
$\left[ 0,4 \right)$
3 )
$\left[ -\frac{1}{2},3 \right]$
4 )
$\left[ -\frac{1}{2},4 \right)$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...