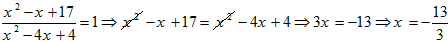** فصل 3: حدهای نامتناهی- حد در بی‌نهایت
حسابان (2)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
اگر نمودار تابع $f(x)=\frac{{{x}^{2}}-x+{{k}^{2}}+1}{{{x}^{2}}-4x+k}$ فقط یک مجانب قائم داشته باشد، این نمودار مجانب افقی خود را در نقطه‌ای با کدام طول قطع می‌کند؟
$-\frac{13}{3}$
2 )
$-\frac{3}{5}$
3 )
$\frac{3}{5}$
4 )
$\frac{13}{3}$
پاسخ تشریحی :
تحلیل ویدئویی تست
عباس ابراهیمی علویجه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...