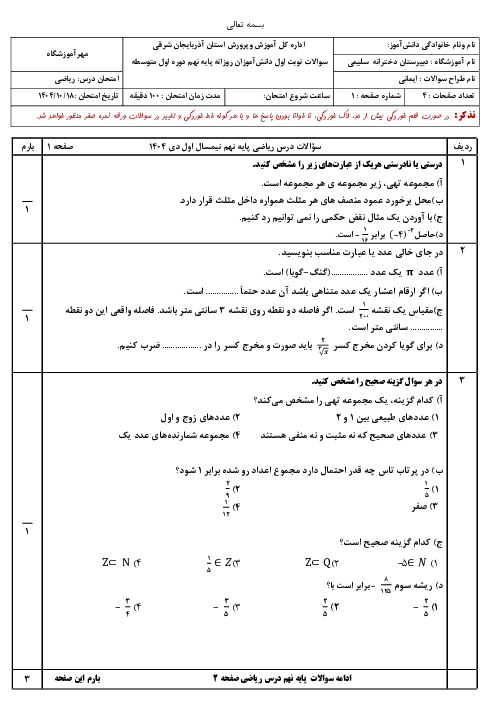
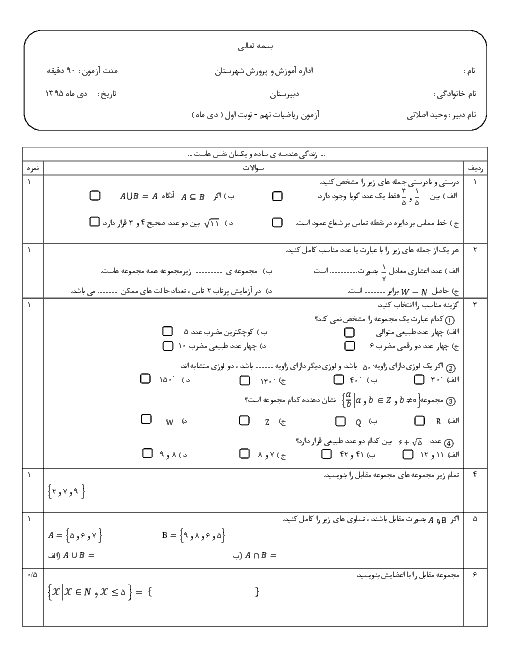
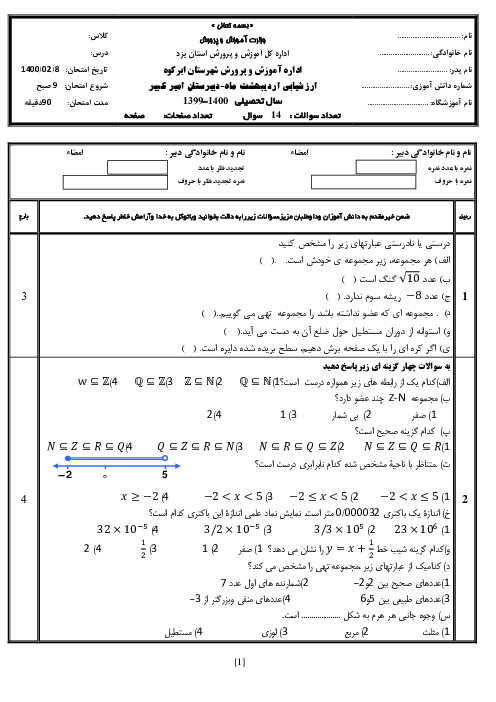
خط $y = 3b$ عمود بر محور عرض‌هاست. یعنی محور عرض‌ها را در $3b$ قطع می‌کند. از آن‌جا که نقطهٔ A روی خط $y = 3b$ است. بنابراین:

$2b + 5 = 3b \Rightarrow b = 5$

مختصات نقطهٔ A با مقدار $b=5$ برابر است با:

$A = \left[ {\begin{array}{*{20}{c}}
  {3 \times 5 - 1} \\ 
  {2 \times 5 + 5} 
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
  {14} \\ 
  {15} 
\end{array}} \right]$

حالا مقدار b را در نقطهٔ $\sqrt {{b^2} - 16} $ قرار می‌دهیم:

$\sqrt {{b^2} - 16}  = \sqrt {{5^2} - 16}  = \sqrt {25 - 16}  = \sqrt 9  = 3$

مختصات نقطهٔ موردنظر برابر با $\left[ {\begin{array}{*{20}{c}}
  0 \\ 
  3 
\end{array}} \right]$ است.

دو نقطهٔ $A = \left[ {\begin{array}{*{20}{c}}
  {14} \\ 
  {15} 
\end{array}} \right]$ و $B = \left[ {\begin{array}{*{20}{c}}
  0 \\ 
  3 
\end{array}} \right]$ را داریم:

$a = \frac{{3 - 15}}{{0 - 14}} = \frac{{ - 12}}{{ - 14}} = \frac{6}{7}$

حالا معادلهٔ خط با شیب $\frac{6}{7}$ و یک نقطهٔ $\left[ {\begin{array}{*{20}{c}}
  0 \\ 
  3 
\end{array}} \right]$ را می‌نویسیم:

$y - 3 = \frac{6}{7}(x - 0)$

$ \Rightarrow y - 3 = \frac{6}{7}x \Rightarrow y - \frac{6}{7}x = 3$