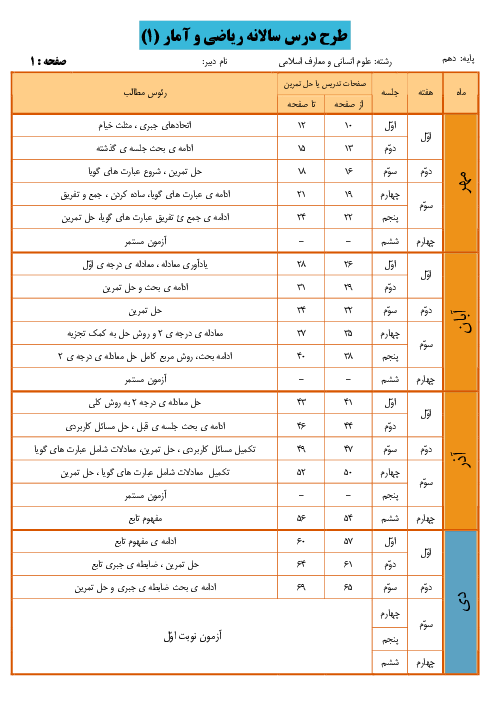
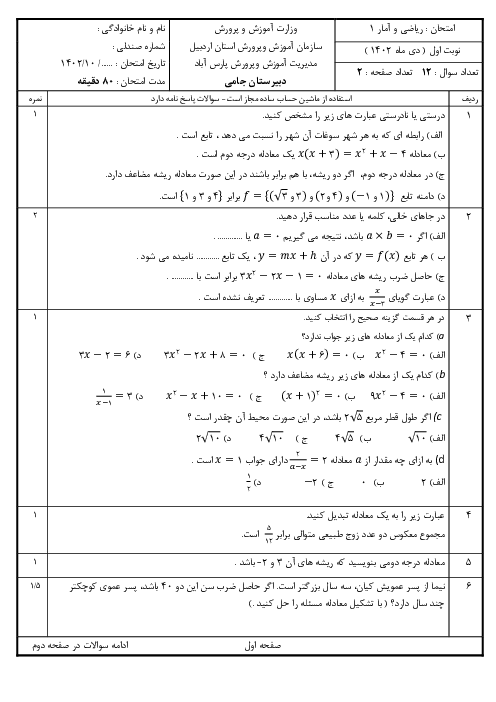
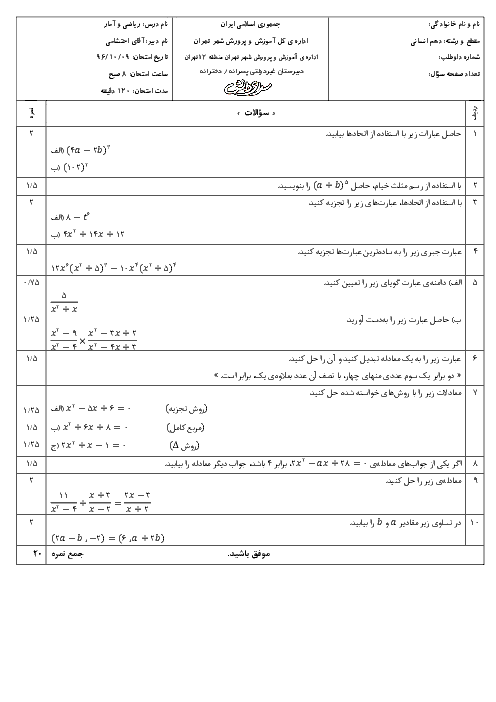
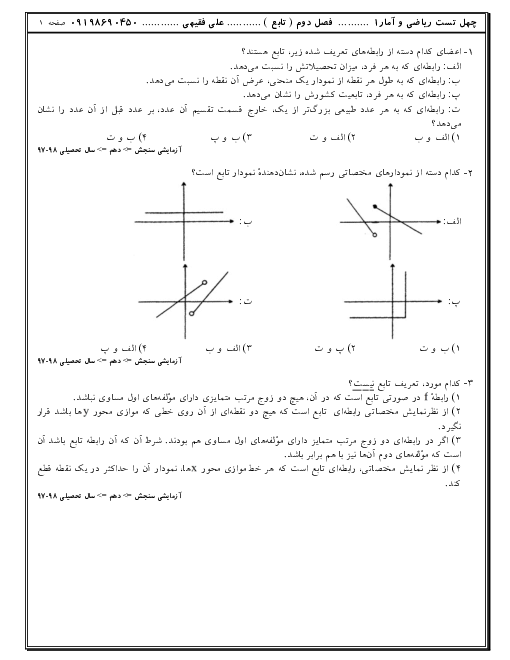
درس 4: رسم تابع درجۀ 2
ریاضی و آمار (1)
دهم
متوسطه دوم نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
اگر معادلهٔ درآمد یک شرکت $R(x) = - \frac{1}{2}{x^2} + 100x$ و معادلهٔ هزینهٔ آن $C(x) = 20x + 3000$ باشد، در این صورت ماکسیمم سودی که نصیب شرکت میشود، کدام است؟
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!