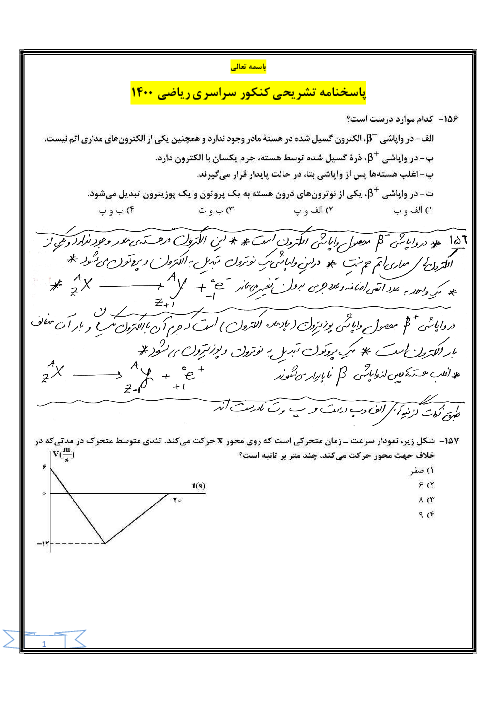
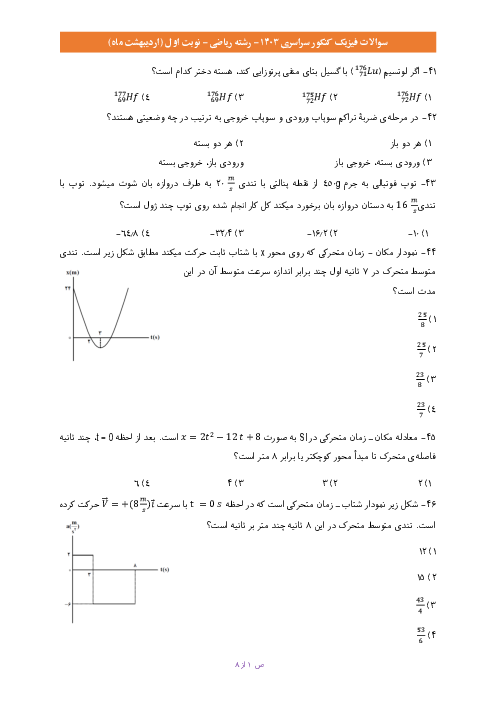
در لحظهٔ ، خط مماس بر نمودار مکان - زمان افقی است. بنابراین سرعت در این لحظه برابر با صفر است.

با استفاده از معادلهٔ سرعت - جابه‌جایی، داریم:

$V{}_1^2 - {V'^2} = 2a({x_1} - x')$

$ \Rightarrow {20^2} - 0 = 2a(0 - ( - 50)) \Rightarrow a = 4m/{s^2}$

از طرف دیگر چون در 8 ثانیهٔ ابتدایی حرکت، سرعت متوسط برابر با صفر است، در حرکت با شتاب ثابت در مسیری مستقیم می‌توان نوشت:

${V_{av}} = \frac{{{V_8} + {V_0}}}{2} = 0 \Rightarrow {V_8} =  - {V_0} \Rightarrow a \times 8 + {V_0} =  - {V_0}\xrightarrow{{a = 4m/{s^2}}}{V_0} =  - 16m/s$

در حرکت با شتاب ثابت داریم:

${V'_{av}} = \frac{{{V_{t'}} + {V_0}}}{2} = \frac{{20 + ( - 16)}}{2} \Rightarrow {V'_{av}} = 2m/s$