دو متحرک در مبدأ زمان، از مبدأ محور می‌گذرند و نمودار سرعت - زمان آنها مطابق شکل است. در بازهٔ زمانی که دو متحرک در خلاف جهت هم حرکت می‌کنند، فاصلهٔ بین آنها چگونه… | فیزیک کنکور سراسری شماره 296639 - گاما

گاما رو نصب کن!

درحال دریافت اطلاعات ...

{{ successMsg }}

{{ errorMsg }}

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت دوم نمونه سوال گام به گام سوالات امتحان نهایی کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نوبت اول تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

سینماتیک فیزیک کنکور سراسری دوره دوم متوسطه- نظری علوم ریاضی

دو متحرک در مبدأ زمان، از مبدأ محور می‌گذرند و نمودار سرعت - زمان آنها مطابق شکل است. در بازهٔ زمانی که دو متحرک در خلاف جهت هم حرکت می‌کنند، فاصلهٔ بین آنها چگونه تغییر می‌کند؟

1 )

48 متر افزایش می‌یابد.

2 )

48 متر کاهش می‌یابد.

3 )

64 متر افزایش می‌یابد.

4 )

64 متر کاهش می‌یابد.

نمایش پاسخ

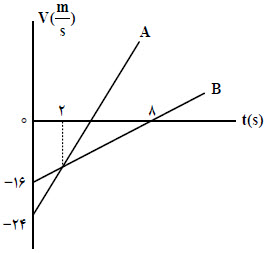
حرکت در خلاف جهت هم $ \leftarrow $ سرعت‌های مختلف ${v_A} \gt 0\,,\,{v_B} \lt 0 \Rightarrow ({t_1} - 8)$

$B:\begin{array}{*{20}{c}}
{\Delta t} \\
{(0 - 8)\,8} \\
{(0 - 2)\,2}
\end{array}\,\,\,\,\,\,\,\,\begin{array}{*{20}{c}}
{\Delta v} \\
{t16\,( - 16 \to 0)} \\
{\underbrace ?_4( - 16 \to ?)}
\end{array}$
$A:\begin{array}{*{20}{c}}
{(0 - 2)\,\,2} \\
{(0 - {t_1})\,\,\underbrace ?_6}
\end{array}\,\,\,\,\,\,\,\,\begin{array}{*{20}{c}}
{8\,\,( - 24 \to - 16)} \\
{24\,\,( - 24 \to 0)}
\end{array}$

چون دو متحرک در $t = 0$ در یک مکان بود. و در $t = 2$ سرعت‌هایشان برابر می‌شود، لذا در $t = 4$ دو باره در یک مکان قرار دارند و در بازه $(4 - 6)$ ، $B$ مقدار بیشتری در خلاف جهت $x$ حرکت می‌کند و در $t = 6$ وضعیت قرارگیری دو متحرک نقطهٔ $A$ تا نقطهٔ $B$ است. لذا در بازه $(6 - 8)$ که $\Delta {x_B} \lt 0$ و $\Delta {x_A} \gt 0$ است، فاصله دو متحرک افزایش خواهیدیافت

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

تحلیل ویدئویی برای این تست ثبت نشده است!

با گنجینه سوال، آزمون دلخواهتو بساز

مجموعه سوالات تستی فیزیک کنکور سراسری 10 سال اخیر | دهم | فصل 1: فیزیک و اندازه‌گیری

7 صفحه

مجموعه سوالات تستی فیزیک کنکور سراسری 10 سال اخیر | دهم | فصل 1: فیزیک…

مهرداد رستمی

رایـــــگان

حل تشریحی سوالات فیزیک کنکور نوبت اردیبهشت 1403 رشته علوم ریاضی

8 صفحه

حل تشریحی سوالات فیزیک کنکور نوبت اردیبهشت 1403 رشته علوم ریاضی

حمزه مشعل پور

سوالات مسابقات جهانی PhysicsBOWl

3 صفحه

سوالات مسابقات جهانی PhysicsBOWl

عباس ابراهیمی علویجه

مجموعه سوالات تستی فیزیک کنکور سراسری 10 سال اخیر | دهم | فصل 3: کار، انرژی و توان

14 صفحه

مجموعه سوالات تستی فیزیک کنکور سراسری 10 سال اخیر | دهم | فصل 3: کار،…

مهرداد رستمی

سوالات فیزیک کنکور سراسری اردیبهشت 1403 رشته ریاضی

8 صفحه

سوالات فیزیک کنکور سراسری اردیبهشت 1403 رشته ریاضی

حمزه مشعل پور

مجموعه سوالات تستی فیزیک کنکور سراسری 10 سال اخیر | دهم | فصل 2: ویژگی‌های فیزیکی مواد، فشار و شناوری

28 صفحه

مجموعه سوالات تستی فیزیک کنکور سراسری 10 سال اخیر | دهم | فصل 2: ویژگی‌های…

مهرداد رستمی

رایـــــگان

تحلیل سوالات درس فیزیک کنکور سراسری ریاضی نوبت اردیبهشت 1403

8 صفحه

تحلیل سوالات درس فیزیک کنکور سراسری ریاضی نوبت اردیبهشت 1403

عزیزالله رحمت پور

تست های آمادگی کنکور فیزیک یازدهم و دوازدهم با پاسخ تشریحی

51 صفحه

تست های آمادگی کنکور فیزیک یازدهم و دوازدهم با پاسخ تشریحی

محمدصادق طاهری

سوالات فیزیک کنکور سراسری نوبت تیر 1403 رشته ریاضی

9 صفحه

سوالات فیزیک کنکور سراسری نوبت تیر 1403 رشته ریاضی

حمزه مشعل پور

پاسخنامه تشریحی فیزیک کنکور سراسری داخل کشور در تیر ماه 1403 | گروه آزمایشی علوم ریاضی

38 صفحه

پاسخنامه تشریحی فیزیک کنکور سراسری داخل کشور در تیر ماه 1403 | گروه آزمایشی…

احسان احمدی نژاد

موارد بیشتر

موارد بیشتر

ارسال فایل

حل سوالات فیزیک در کنکور

فرق بین یک جسم بدون بار و جسم خنثی چیست؟

تخمین مرتبه بزرگی چیست و چطور محاسبه می‌شود؟

موارد بیشتر

ارسال پرسش

موارد بیشتر