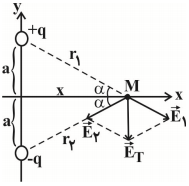
همان‌طور كه می‌دانید عمـود منصـف خط واصل دو بار محور x است و به این مجموعه دوقطبی الكتریكی گفتـه می‌شود. مطابق شكل، میدان براینـد در نقطهٔ دلخواه M برایند میدان‌های $\overrightarrow{{{E}_{1}}}$ و $\overrightarrow{{{E}_{2}}}$ است.

${{r}_{1}}={{r}_{2}}=r=\sqrt{{{a}^{2}}+{{x}^{2}}},{{E}_{1}}={{E}_{2}}=E=\frac{kq}{{{r}^{2}}}=\frac{kq}{{{a}^{2}}+{{x}^{2}}}$

برای محاسبهٔ بردار میدان الكتریكی برایند $(\overrightarrow{{{E}_{T}}})$ باید میدان‌های $\overrightarrow{{{E}_{1}}}$ و $\overrightarrow{{{E}_{2}}}$ را به‌صورت برداری بنویسیم. از آن‌جا كه اندازهٔ میدان‌های $\overrightarrow{{{E}_{1}}}$ و $\overrightarrow{{{E}_{2}}}$  باهم برابر است، زاویهٔ آن‌ها با محور افقی (x) یكسان و برابر $\alpha $ اسـت می‌توان گفت كه مؤلفه‌های افقی میدان الكتریكی یعنی ${{E}_{1x}}$ و ${{E}_{2x}}$ یـكدیگـر را خنثی می‌كنند و تنها كافی است كه مؤلفه‌های قائم را حساب كنیم:

${{E}_{1y}}={{E}_{2y}}=E\sin \alpha ,\sin \alpha =\frac{a}{\sqrt{{{a}^{2}}+{{x}^{2}}}}$

${{E}_{T}}=2{{E}_{1y}}=2E\sin \alpha =2\times \frac{kq}{({{a}^{2}}+{{x}^{2}})}\times \frac{a}{\sqrt{{{a}^{2}}+{{x}^{2}}}}\Rightarrow {{E}_{T}}=\frac{2kqa}{{{({{a}^{2}}+{{x}^{2}})}^{\frac{3}{2}}}}$