درس 2: حل معادلۀ درجۀ 2 و کاربردها
ریاضی و آمار (1)
دهم
دوره دوم متوسطه- نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
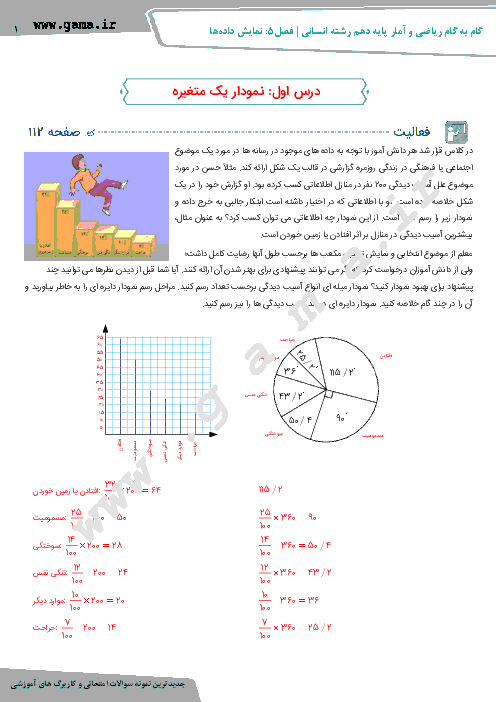
برای تولیدات یک کارگاه تولیدی در یک ماه، رابطۀ بین تعداد کالای فروخته شده (x) و قیمت فروش هر کالا (p) به‌صورت نمودار زیر است. اگر تابع هزینۀ تولید x واحد کالا به‌صورت $C(x) = {x^2} + 5x + 1000$ باشد، رابطۀ سود این کارگاه برحسب x کدام است؟
1 )
$P(x) = - {1 \over 2}{x^2} + 30x - 1000$
2 )
$P(x) = - {1 \over 2}{x^2} + 40x - 1000$
3 )
$P(x) = - {3 \over 2}{x^2} + 40x - 1000$
$P(x) = - {3 \over 2}{x^2} + 30x - 1000$
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...