درس 1: مفاهیم اولیه و زاویهها در دایره
هندسه (2)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
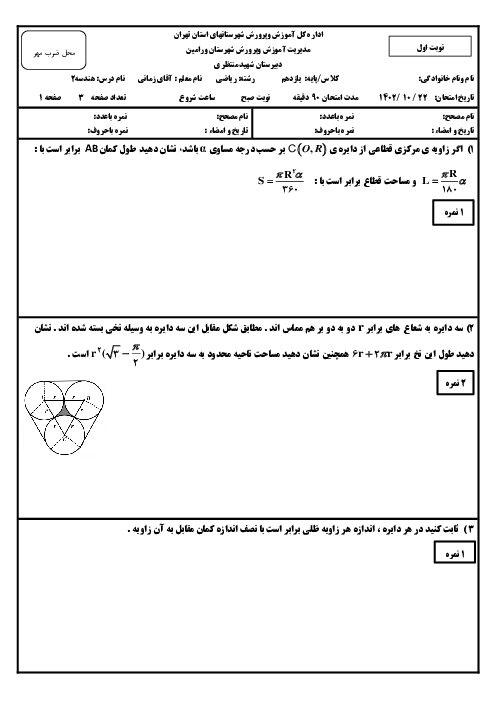
در شکل زیر، اگر O مرکز دایره باشد و $PM=PN$، اندازهی زایهی $\alpha $ چقدر است؟
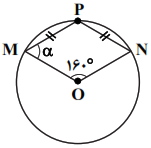
${{50}^{{}^\circ }}$
2 )
${{60}^{{}^\circ }}$
3 )
${{70}^{{}^\circ }}$
4 )
${{80}^{{}^\circ }}$
پاسخ تشریحی :