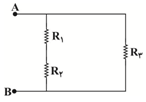
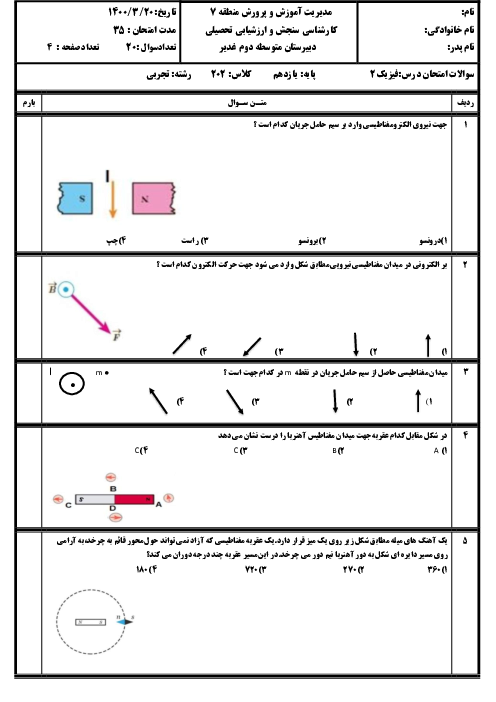
در این مدار، مقاومت ${{R}_{1}}$ و ${{R}_{2}}$ با يكديگر متوالی هستند و معادل آنها برابر با ${{R}_{1}}+{{R}_{2}}$ میشود و مقاومت معادل آنها با مقاومت ${{R}_{3}}$ موازی است. بنابراين مقاومت معادل مجموعه بهصورت زير محاسبه میشود.
${{R}_{eq}}=\frac{{{R}_{1,2}}\times {{R}_{3}}}{{{R}_{1,2}}+{{R}_{3}}}\xrightarrow[{{R}_{eq}}={{R}_{2}}]{{{R}_{1,2}}={{R}_{1}}+{{R}_{2}}}$
${{R}_{2}}=\frac{({{R}_{1}}+{{R}_{2}})\times {{R}_{3}}}{({{R}_{1}}+{{R}_{2}})+{{R}_{3}}}$
$\Rightarrow {{R}_{1}}{{R}_{2}}+R_{2}^{2}+{{R}_{2}}{{R}_{3}}={{R}_{1}}{{R}_{3}}+{{R}_{2}}{{R}_{3}}$
$\Rightarrow R_{2}^{2}={{R}_{1}}{{R}_{3}}-{{R}_{1}}{{R}_{2}}$
$\Rightarrow R_{2}^{2}={{R}_{1}}({{R}_{3}}-{{R}_{2}})\Rightarrow {{R}_{1}}=\frac{R_{2}^{2}}{({{R}_{3}}-{{R}_{2}})}$