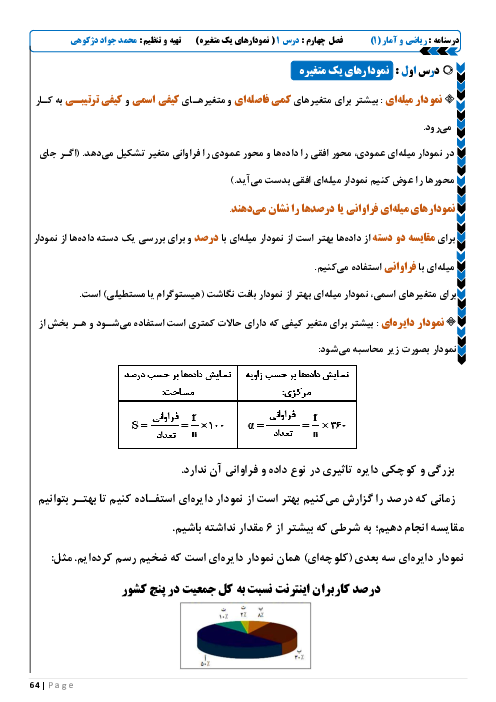
درس 2: ضابطۀ جبری تابع
ریاضی و آمار (1)
دهم
دوره دوم متوسطه- نظری
ادبیات و علوم انسانی
درسنامه آموزشی این مبحث
دامنه و برد تابع $\left\{ \matrix{ f:A \to B \hfill \cr y = {{x + 1} \over {x - 2}} \hfill \cr} \right.$ به‌صورت $A = \left\{ { - 2,a,1} \right\}$ و ${R_f} = \left\{ {b,{1 \over 4},0} \right\}$ است. حاصل $a + b$ کدام است؟
تحلیل ویدئویی تست
عادل علی پناه 
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...