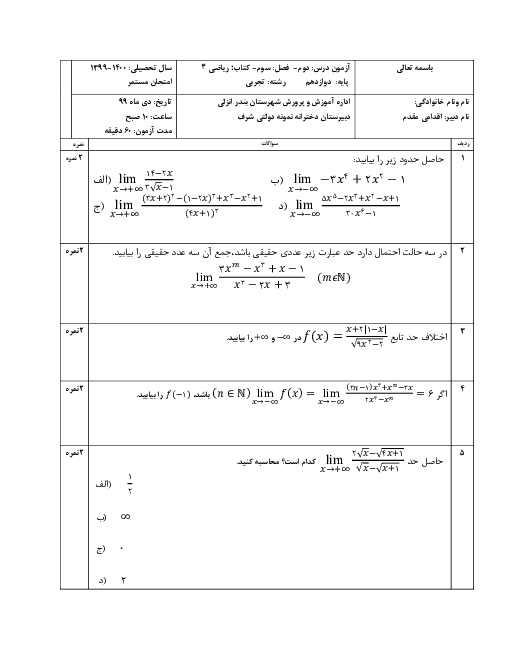
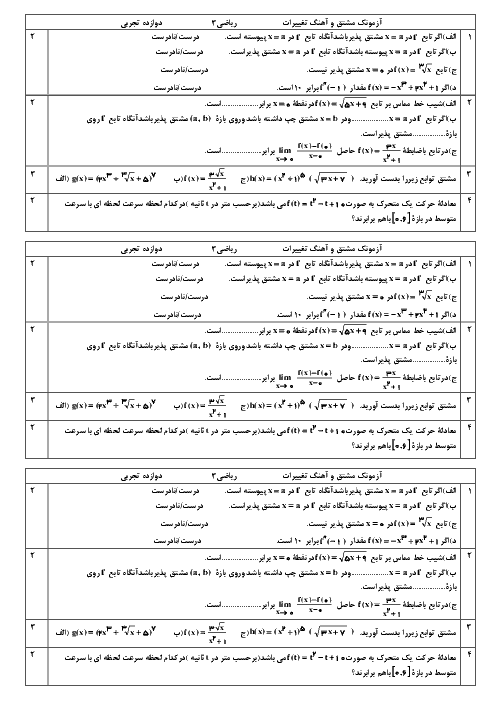
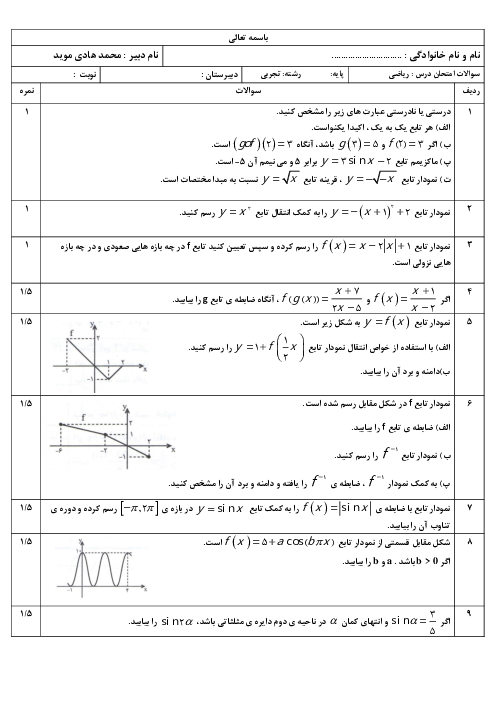
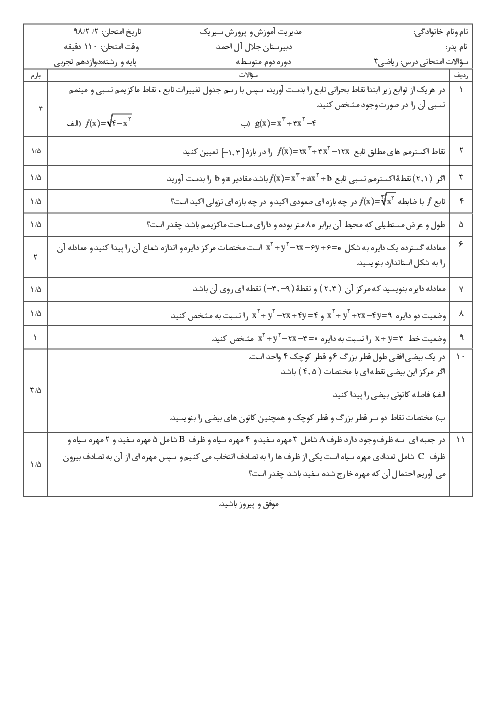
اگر $f(x) = \sqrt {4 - 2x} $ و $g(x) = {x^2} + 2x - 1$ باشد،
الف) دامنهٔ تابع gof را با استفاده از تعریف به دست آورید.
ب) مقدار $gof(2) - \frac{f}{g}(0)$ تعیین کنید.
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...