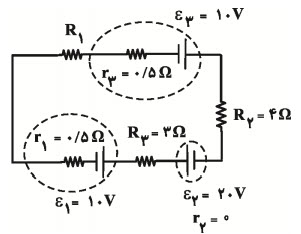
چون در این مدار ${{\varepsilon }_{2}}$ و ${{\varepsilon }_{3}}$ هم جهت‌اند و ${{\varepsilon }_{1}}$ خلاف جهت آن‌ها بسته شده است و ${{\varepsilon }_{2}}+{{\varepsilon }_{3}}\gt {{\varepsilon }_{1}}$ است، جريان ساعتگرد است و مقدار آن برابر است با:

$I=\frac{{{\varepsilon }_{2}}+{{\varepsilon }_{3}}-{{\varepsilon }_{1}}}{{{R}_{eq}}+{{r}_{1}}+{{r}_{2}}+{{r}_{3}}}=\frac{20}{{{R}_{1}}+7+1}=\frac{20}{{{R}_{1}}+8}$

مجموع توان خروجی مولدهای ${{\varepsilon }_{2}}$ و ${{\varepsilon }_{3}}$ برابر است با:

$P={{P}_{2}}+{{P}_{3}}=({{\varepsilon }_{2}}I-{{r}_{2}}{{I}^{2}})+({{\varepsilon }_{3}}I-{{r}_{3}}{{I}^{2}})$

$\xrightarrow{{{r}_{2}}=0}P=58=20I+(10I-\frac{1}{2}{{I}^{2}})=30I-\frac{{{I}^{2}}}{2}$

$\Rightarrow 58=30I-\frac{{{I}^{2}}}{2}\Rightarrow {{I}^{2}}-60I+116=0$

$\Rightarrow (I-2)(I-58)=0\Rightarrow \left\{ \begin{matrix} I=2A  \\ I=58A  \\ \end{matrix} \right.$

$\xrightarrow{I=\frac{20}{{{R}_{1}}+8}}\left\{ \begin{matrix} \frac{20}{{{R}_{1}}+8}=2\Rightarrow {{R}_{1}}=2\Omega  ق . ق \\ \frac{20}{{{R}_{1}}+8}=58\xrightarrow{{{R}_{1}}\ge 0}{{R}_{1}}\simeq -7/66  ق . ق . غ \\ \end{matrix} \right.$