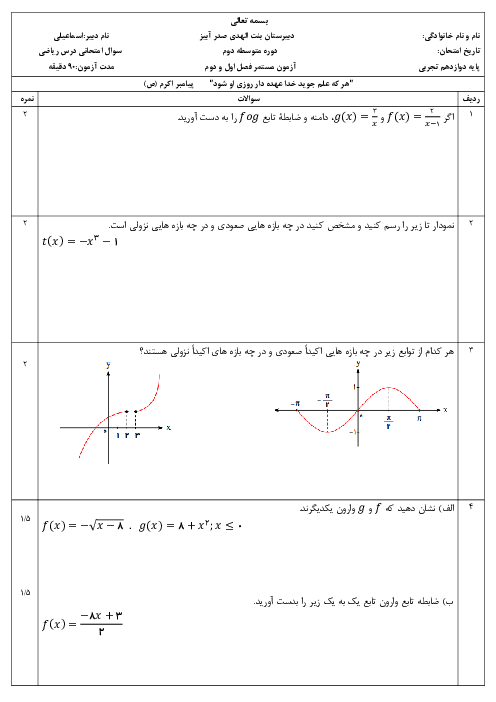
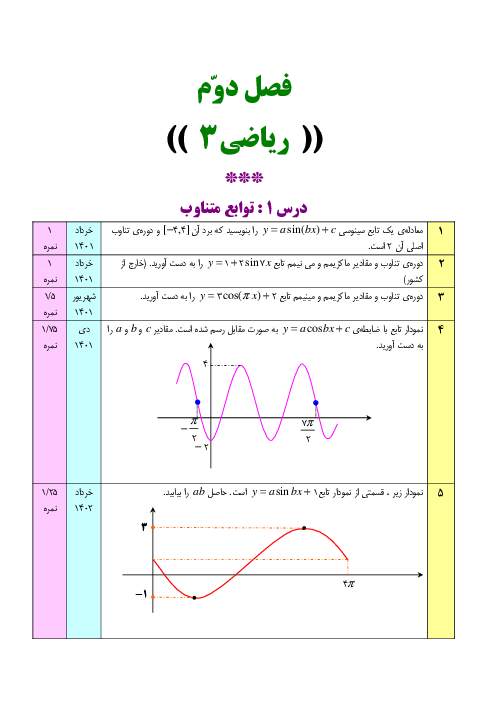
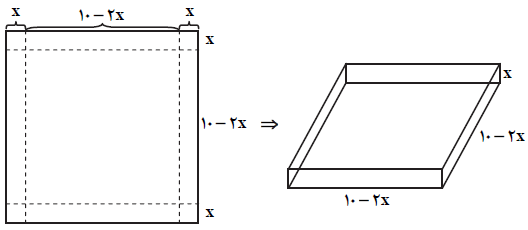
ورق فلزی مربعشكلی به طول ضلع ۱۰ را در نظر بگيريد. مطابق شكل میخواهيم از چهار گوشهی آن مربعهای كوچكی به ضلع $x$ برش بزنيم و آنها را كنار بگذاريم، سپس با تا كردن ورق در امتداد خطچينهای مشخص شده، يک جعبهی در باز بسازيم. بيشترين مقدار ممكن برای حجم اين جعبه كدام است؟
1 )
$\frac{2000}{9}$
2 )
$\frac{1000}{27}$
$\frac{2000}{27}$
4 )
$\frac{1000}{9}$
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!