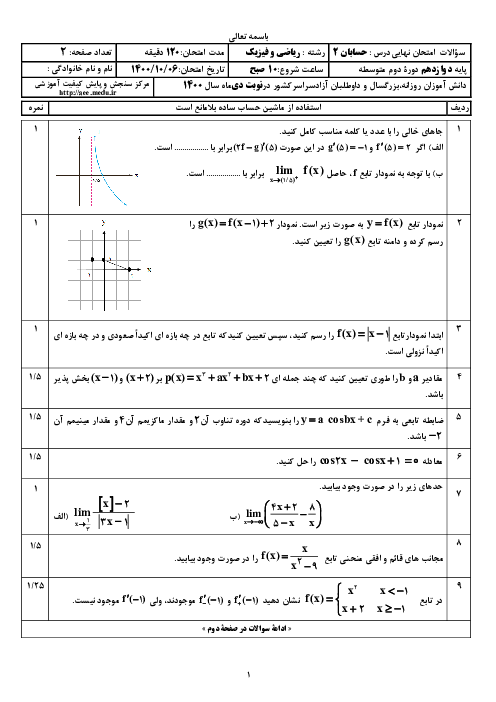
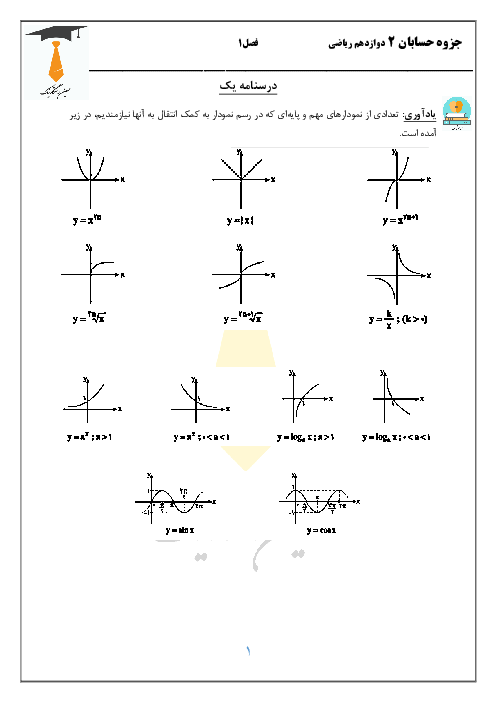
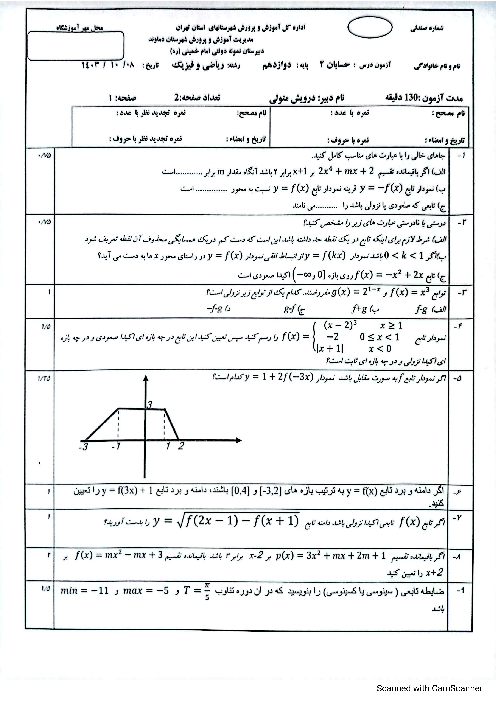
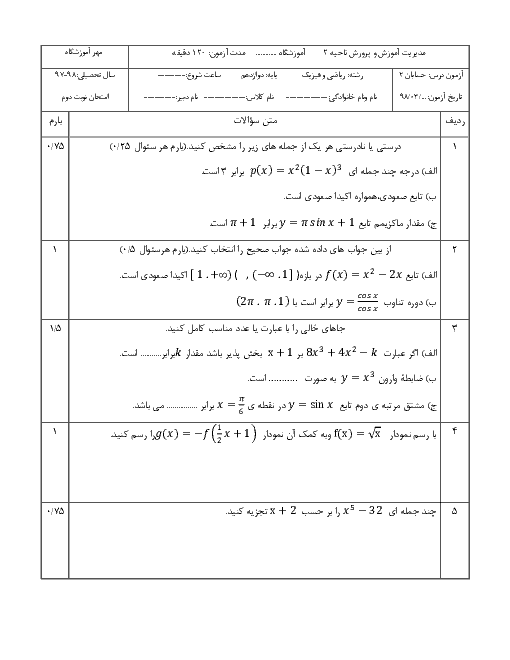
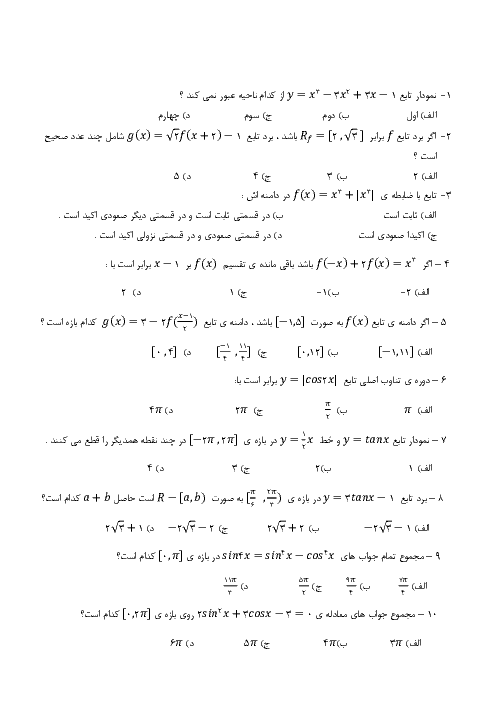$\begin{gathered}
\frac{{2\left( {\tan x - \sqrt {\tan x} } \right)\left( {\sqrt {\tan x} {\text{ }} + \tan x} \right)}}{2} = \frac{{2{{\sin }^2}x}}{{\left( {1 + \sin x} \right)\left( {1 - \sin x} \right)}} \to {\tan ^2}x - \tan x = \frac{{2{{\sin }^2}x}}{{1 - {{\sin }^2}x}} \hfill \\
{\tan ^2}x - \tan x = \frac{{2{{\sin }^2}x}}{{co{s^2}x}} = 2{\tan ^2}x \to {\tan ^2}x + \tan x = 0 \to \xcancel{{\tan x = {\text{ }} - 1{\text{ }}}},\xcancel{{\tan x = 0}} \hfill \\
\end{gathered} $
نکته:معادله شامل ${\sqrt {\tan x} }$ است بنابراین $\tan x = - 1$ غیرقابل قبول است.
از طرفی به ازای $\tan x = 0$ مخرج برابر صفر میشود لذا این جواب نیز غیرقابل قبول است.
بنابراین معادله جواب ندارد.