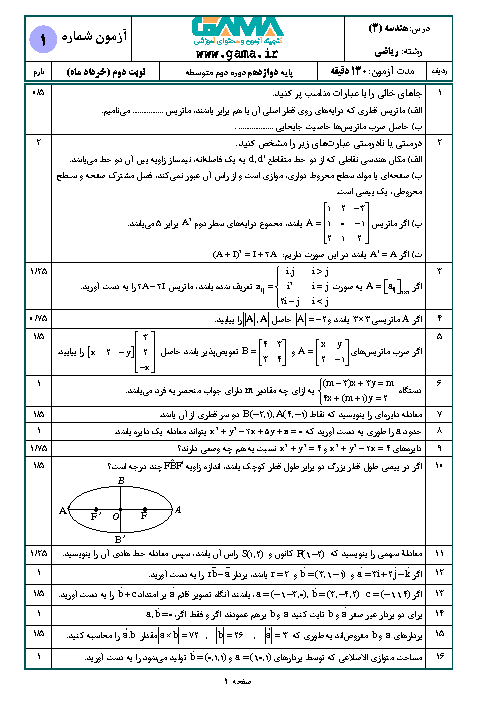
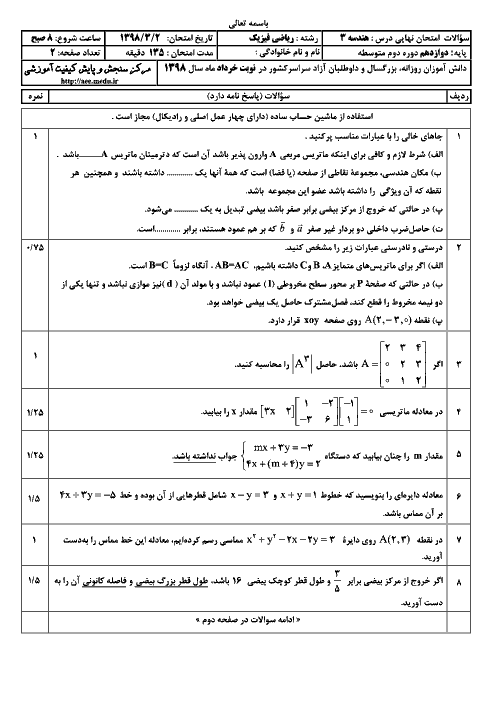
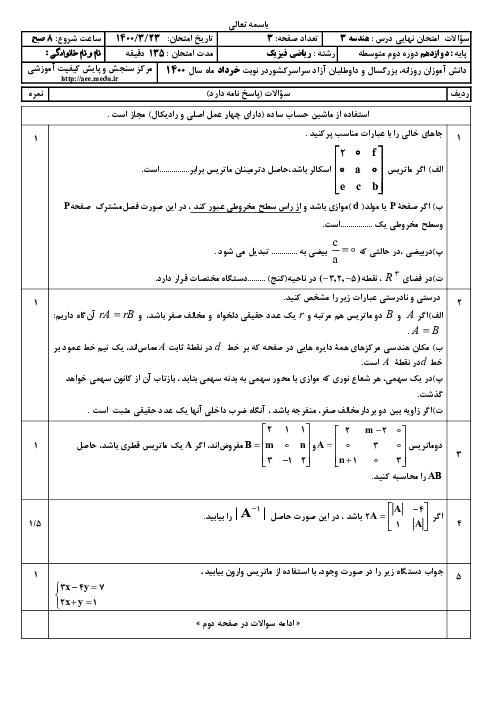
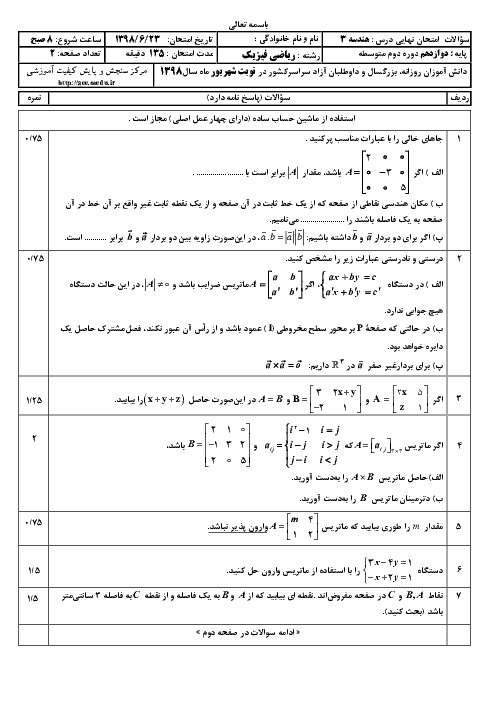
برای آنكه دستگاه بی‌شمار جواب داشته باشد، بايد دو خط $ax-3y=1$ و $20x+by=5$ بر هم منطبق باشند:

$\frac{a}{20}=\frac{-3}{b}=\frac{1}{5}\Rightarrow \left\{ \begin{matrix} a=4  \\ b=-15  \\ \end{matrix} \right.$

حال بین گزینه‌ها، دستگاه معادلاتی را انتخاب می‌کنیم که دترمینان ماتریس ضرایب آن مخالف صفر باشد تا جواب منحصربه‌فرد داشته باشد.

$1)\left| \begin{matrix} \begin{matrix} 15 & -4  \\ \end{matrix}  \\ \begin{matrix} b & a  \\ \end{matrix}  \\ \end{matrix} \right|=\left| \begin{matrix} \begin{matrix} 15 & -4  \\ \end{matrix}  \\ \begin{matrix} -15 & 4  \\ \end{matrix}  \\ \end{matrix} \right|=0$

$2)\left| \begin{matrix} \begin{matrix} a & -15  \\ \end{matrix}  \\ \begin{matrix} 4 & b  \\ \end{matrix}  \\ \end{matrix} \right|=\left| \begin{matrix} \begin{matrix} 4 & -15  \\ \end{matrix}  \\ \begin{matrix} 4 & -15  \\ \end{matrix}  \\ \end{matrix} \right|=0$

$3)\left| \begin{matrix} \begin{matrix} a & 15  \\ \end{matrix}  \\ \begin{matrix} b & a  \\ \end{matrix}  \\ \end{matrix} \right|=\left| \begin{matrix} \begin{matrix} 4 & 15  \\ \end{matrix}  \\ \begin{matrix} -15 & 4  \\ \end{matrix}  \\ \end{matrix} \right|\ne 0$

$4)\left| \begin{matrix} \begin{matrix} a & b  \\ \end{matrix}  \\ \begin{matrix} 3a & 3b  \\ \end{matrix}  \\ \end{matrix} \right|=0$