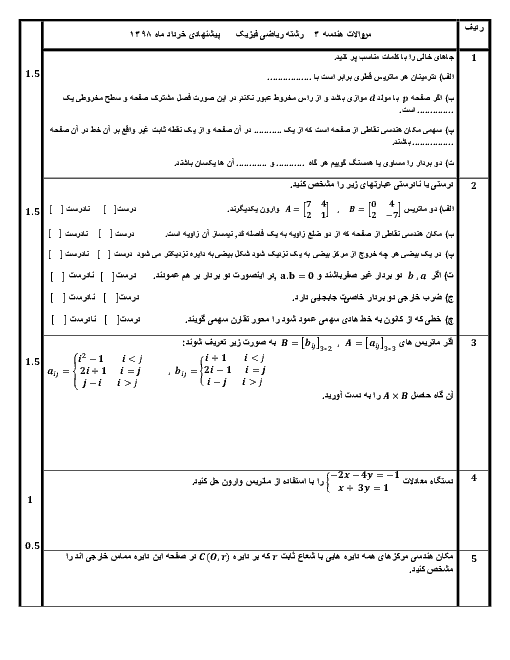
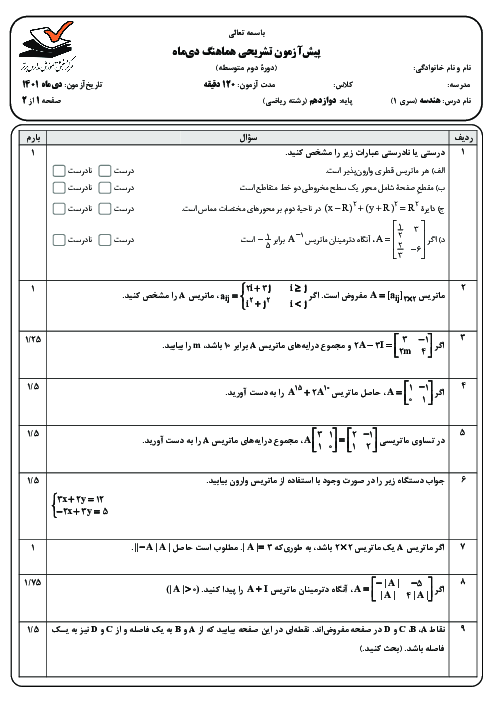
طرفين معادله را از سمت راست در ${{\left[ \begin{matrix} \begin{matrix} 1 & 2  \\ \end{matrix}  \\ \begin{matrix} 3 & 4  \\ \end{matrix}  \\ \end{matrix} \right]}^{-1}}$ ضرب می‌کنیم تا ماتریس $\left[ \begin{matrix} \begin{matrix} a & b  \\ \end{matrix}  \\ \begin{matrix} c & d  \\ \end{matrix}  \\ \end{matrix} \right]$ به‌دست می‌آید.

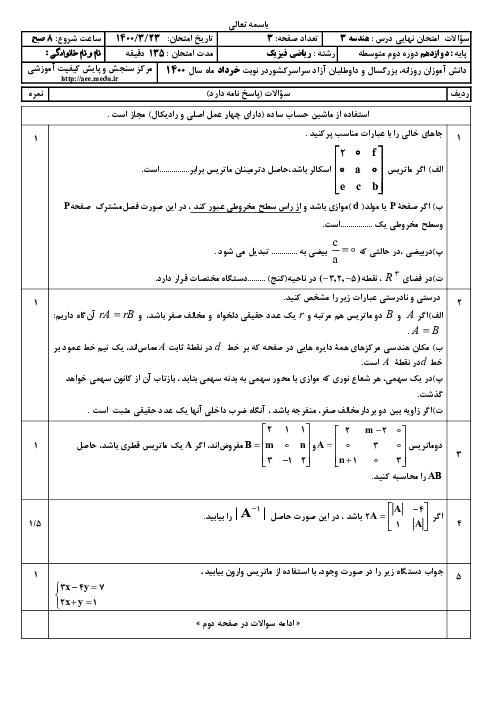
$\left( \left[ \begin{matrix} \begin{matrix} a & b  \\ \end{matrix}  \\ \begin{matrix} c & d  \\ \end{matrix}  \\ \end{matrix} \right]\left[ \begin{matrix} \begin{matrix} 1 & 2  \\ \end{matrix}  \\ \begin{matrix} 3 & 4  \\ \end{matrix}  \\ \end{matrix} \right] \right){{\left[ \begin{matrix} \begin{matrix} 1 & 2  \\ \end{matrix}  \\ \begin{matrix} 3 & 4  \\ \end{matrix}  \\ \end{matrix} \right]}^{-1}}=$$\left[ \begin{matrix} \begin{matrix} 7 & 12  \\ \end{matrix}  \\ \begin{matrix} -11 & -16  \\ \end{matrix}  \\ \end{matrix} \right]{{\left[ \begin{matrix} \begin{matrix} 1 & 2  \\ \end{matrix}  \\ \begin{matrix} 3 & 4  \\ \end{matrix}  \\ \end{matrix} \right]}^{-1}}$

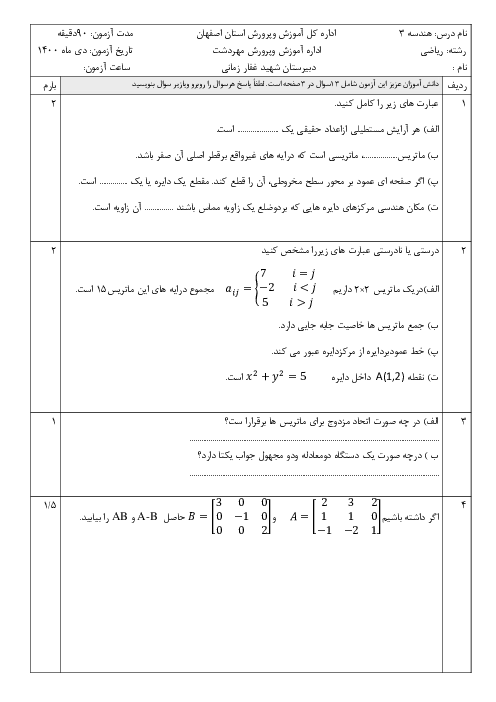
$\left[ \begin{matrix} \begin{matrix} a & b  \\ \end{matrix}  \\ \begin{matrix} c & d  \\ \end{matrix}  \\ \end{matrix} \right]\left( \left[ \begin{matrix} \begin{matrix} 1 & 2  \\ \end{matrix}  \\ \begin{matrix} 3 & 4  \\ \end{matrix}  \\ \end{matrix} \right]{{\left[ \begin{matrix} \begin{matrix} 1 & 2  \\ \end{matrix}  \\ \begin{matrix} 3 & 4  \\ \end{matrix}  \\ \end{matrix} \right]}^{-1}} \right)=$$\left[ \begin{matrix} \begin{matrix} 7 & 12  \\ \end{matrix}  \\ \begin{matrix} -11 & -16  \\ \end{matrix}  \\ \end{matrix} \right]\times \frac{1}{4-6}\left[ \begin{matrix} \begin{matrix} 4 & -2  \\ \end{matrix}  \\ \begin{matrix} -3 & 1  \\ \end{matrix}  \\ \end{matrix} \right]$

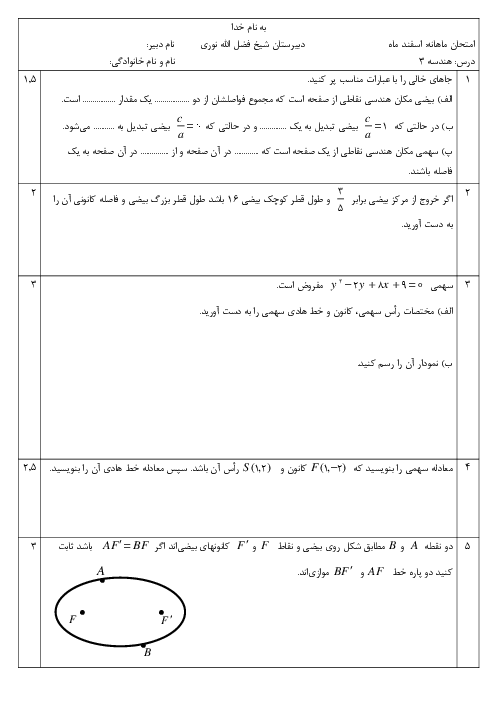
$\Rightarrow \left[ \begin{matrix} \begin{matrix} a & b  \\ \end{matrix}  \\ \begin{matrix} c & d  \\ \end{matrix}  \\ \end{matrix} \right]=-\frac{1}{2}\left[ \begin{matrix} \begin{matrix} -8 & -2  \\ \end{matrix}  \\ \begin{matrix} 4 & 6  \\ \end{matrix}  \\ \end{matrix} \right]=\left[ \begin{matrix} \begin{matrix} 4 & 1  \\ \end{matrix}  \\ \begin{matrix} -2 & -3  \\ \end{matrix}  \\ \end{matrix} \right]$

$\Rightarrow a+b+c+d=0$