راه‌حل اول:

نکته (قانون ضرب احتمال برای سه پیشامد): اگر ${{A}_{1}}$، ${{A}_{2}}$ و ${{A}_{3}}$ پيشامدهايی با احتمال ناصفر باشند، آنگاه:

$P({{A}_{1}}\bigcap {{A}_{2}}\bigcap {{A}_{3}})=P({{A}_{1}})P({{A}_{2}}\left| {{A}_{1}}) \right.P({{A}_{3}}{{\left| ({{A}_{1}}\bigcap A \right.}_{2}}))$

 نكته: در صورتی كه $B$ پيشامدی باشد كه $P(B)\gt 0$، برای هر پيشامد $A$، «احتمال $A$ به‌شرط رخ دادن $B$» به‌شكل زير تعريف می‌شود:

$P(A\left| B)= \right.\frac{P(A\bigcap B)}{P(B)}$

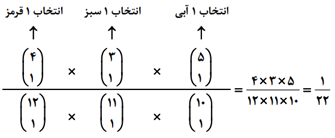
 با توجه به صورت سؤال، احتمال اينكه اولين مهره قرمز، دومی سبز و سومی آبی باشد به‌صورت زير است:

$P$ (دومی سبز $\bigcap $ اولی قرمز $\left| {} \right.$ سومی آبی) $P$ (اولی قرمز $\left| {} \right.$ دومی سبز) $P$ (اولی قرمز)$P$= (سومی آبی $\bigcap $ دومی سبز $\bigcap $ اولی قرمز)) 

$=\frac{4}{12}\times \frac{\frac{4}{12}\times \frac{3}{11}}{\frac{4}{12}}\times \frac{\frac{5}{10}\times (\frac{4}{12}\times \frac{3}{11})}{(\frac{4}{12}\times \frac{3}{11})}=\frac{4}{12}\times \frac{3}{11}\times \frac{5}{10}=\frac{1}{22}$

راه‌حل دوم: احتمال خواسته‌شده به‌صورت زير است: