درس 1: تفکر تجسمی و آشنایی با مقاطع مخروطی
ریاضی (3)
دوازدهم
متوسطه دوم نظری
علوم تجربی
درسنامه آموزشی این مبحث
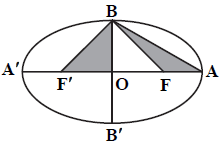
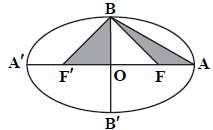
در بيضی مقابل، اگر مساحت مثلث $OB{F}'$ سه برابر مساحت مثلث $ABF$ و قطر كوچک بيضی برابر $4$ باشد، قطر بزرگ بيضی كدام است؟
$\frac{16\sqrt{7}}{7}$
2 )
$4\sqrt{7}$
3 )
$\frac{10\sqrt{7}}{7}$
4 )
$\frac{8\sqrt{7}}{7}$
پاسخ تشریحی :