درس 1: ماتریس و اعمال روی ماتریس‌ها
هندسه (3)
دوازدهم
دوره دوم متوسطه- نظری
علوم ریاضی
درسنامه آموزشی این مبحث
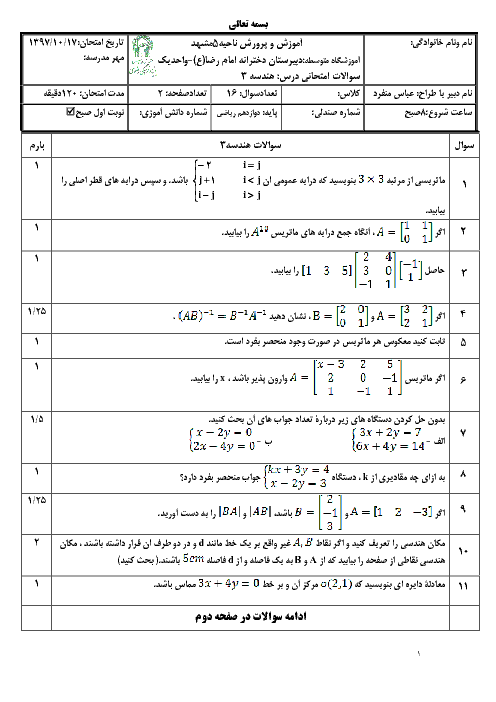
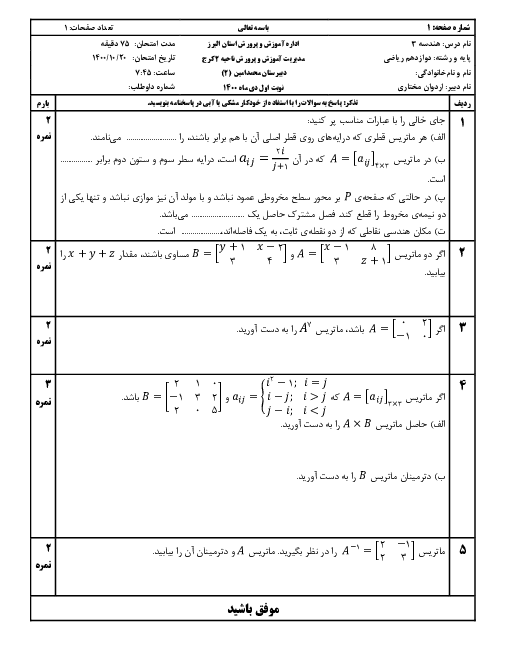
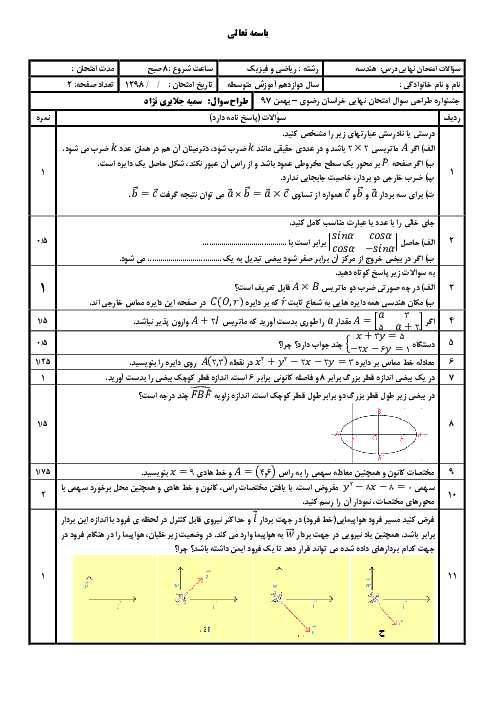
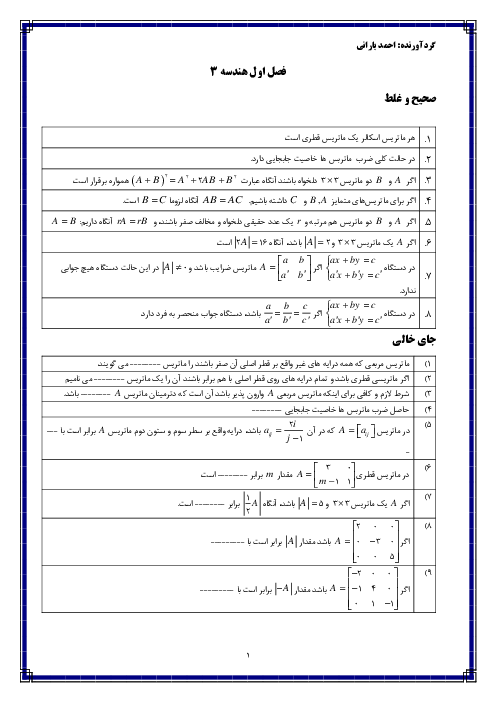
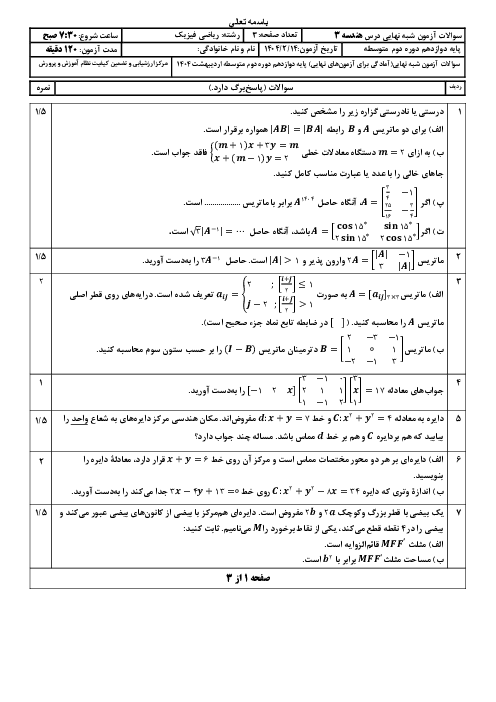
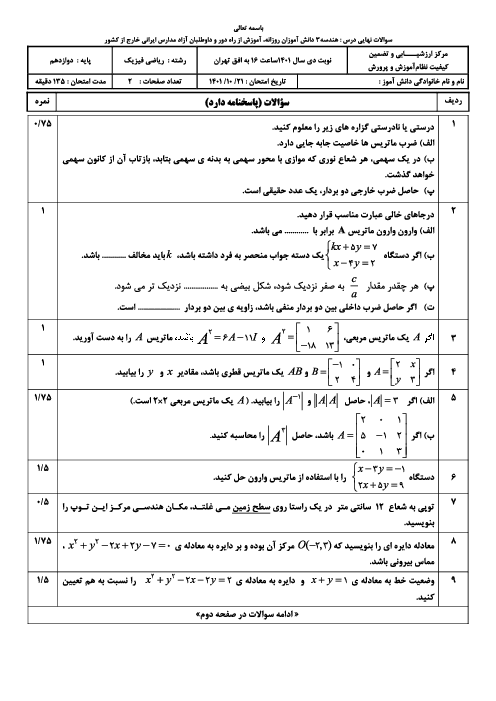
ماتریس‌های $A = \left[ {\begin{matrix} { -1} & m \\ { -2} & m \\ \end{matrix} } \right]$ و $B = \left[ {\begin{matrix} 2 & { -3} \\ 3 & 1 \\ \end{matrix} } \right]$ چنان هستند که $C = 3A + 2B$ ماتریس قطری است. مقدار m و مجموع درایه‌های قطر اصلی ماتریس C را حساب کنید.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...